"Light makes right. " — Andrew Glassner

在第9章中，我们讨论了基于物理的材质理论，以及如何用点源光对它们进行计算。通过此内容，我们可以通过模拟灯光与曲面的交互方式来执行着色计算，以便测量在给定方向上向虚拟相机发送多少辐亮度。 该光谱辐射亮度是场景参考像素颜色，将被转换（第8.2节）到给定像素在最终图像中将具有的显示参考颜色。

实际上，我们需要考虑的互动从不是点源的。我们在第9.13.1节中已经看到，为了正确计算着色，我们必须依照像素的足迹（pixel footprint）计算整个像素覆盖区域上表面BRDF的积分，这是像素区域在表面上的投影。这种集成过程也可以被认为是一种抗锯齿解决方案。我们预先集成，而不是对其频率成分没有约束的着色函数进行采样。

到目前为止，仅呈现了点光源和定向光源的效果，这限制了表面从少数离散方向接收光。这种照明描述不完整。实际上，表面接收来自所有传入方向的光。户外场景不仅仅是被太阳照亮。若是这样，阴影中或背离太阳的所有表面都将是黑色的。天空是由大气中的阳光散射引起的重要光源。通过观察月球的图片可以看到天空的重要性，因为它没有大气层，因此缺少天光。见图10.1。

在阴天，黄昏或黎明时，户外照明都是天空之光。即使在晴朗的日子，当从地球上看时，太阳会对着一个圆锥体，所以它不是无限小的。奇怪的是，太阳和月亮都有相似的角度，大约半度，尽管它们的巨大尺寸差异：太阳的半径比月亮大两个数量级。

实际上，照明永远不会是点光。无穷小实体在某些情况下可用作廉价近似值，或用作更完整模型的构建块。为了形成更逼真的照明模型，我们需要将BRDF响应整合到表面上的整个入射方向半球上。 在实时渲染中，我们更倾向于通过找到闭合形式的解或其近似来求解渲染方程（第11.1节）所需的积分。 我们通常避免平均多个样本（光线），因为这种方法往往要慢得多。 见图10.2。

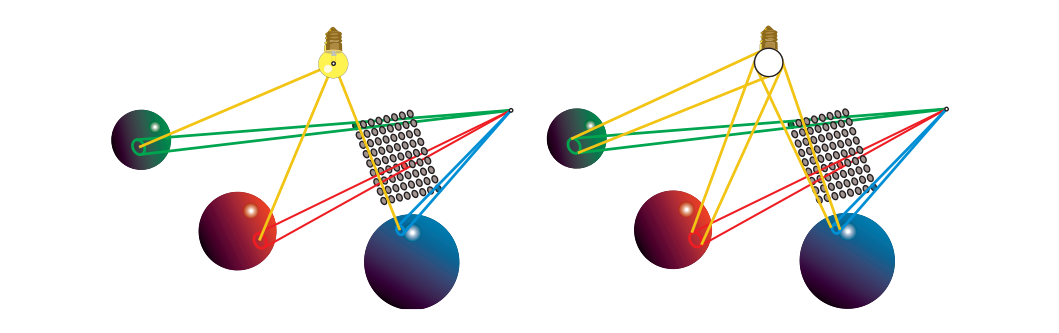
本章致力于探索此类解决方案。特别是，我们希望通过使用各种非功能性光源计算BRDF来扩展我们的着色模型。通常，为了找到廉价的解决方案（或任何根本），我们需要近似光发射器，BRDF或两者。重要的是在感知框架中评估最终的着色结果，了解最终图像中哪些元素最重要，从而为这些元素分配更多的努力。

我们从本章开始，使用公式来集成分析区域光源。这种发射器是场景中的主要光源，负责大部分直接照明强度，因此对于这些，我们需要保留所有选定的材质属性。应该为这样的发射器计算阴影，因为光泄漏将导致明显的伪影。然后，我们研究了表示更一般照明环境的方法，这些环境由进入的半球上的任意分布组成。在这些情况下，我们通常接受更接近的解决方案。环境照明用于大型，复杂但不太强烈的光源。例子包括从天空和云层散射的光，间接光从场景中的大物体反射，以及调光器直接区域光源。这样的发射器对于图像的正确平衡是重要的，否则图像将显得太暗。即使我们考虑间接光源的影响，我们仍然不在全局照明领域（第11章），这取决于场景中其他表面的知识。

10.1 Area Light Sources（区域光源）

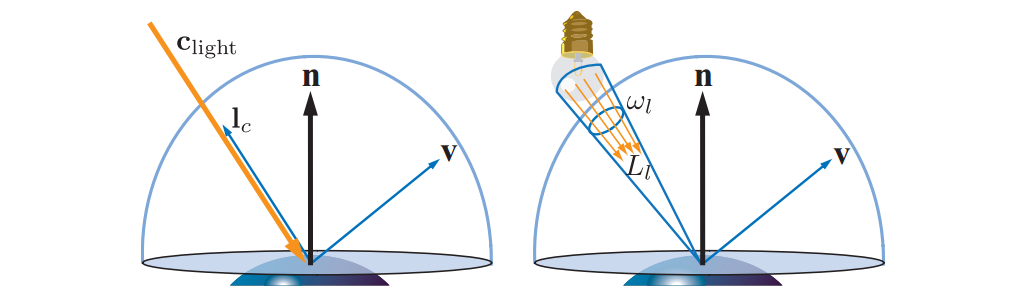
在第9章中，我们描述了理想化的无限小光源：点源和定向。图10.3显示了表面点上的入射半球，以及无穷小源和具有非零尺寸的区域光源之间的差异。左侧的光源使用第9.4节中讨论的定义。它从单个方向$l_c$照亮表面。它的亮度由$\boldsymbol{c}_{light}$表示，定义为白色的朗伯表面朝向光线的反射辐射。点方向或方向光对方向$\boldsymbol{v}$的出射辐射$L_o(\boldsymbol{v})$的贡献是$πf(l_c, v)c_{light}(n·l_c)^+$。或者，区域光源（右侧）的亮度由其辐射亮度$L_1$表示。区域光从表面位置对着一个立体角。它对方向 $\boldsymbol{v}$ 的输出辐射的贡献是在$w_l$上的$f(l, v)L_l(n\cdot l)^+$的积分。

无穷小光源背后的基本近似表达式如下：

$$
L_o(\boldsymbol{v})=\int_{\boldsymbol{l}\in\omega_l}f(\boldsymbol{l,v})L_l(\boldsymbol{n\cdot l})^+d\boldsymbol{l}\approx\pi f(\boldsymbol{l}_c,\boldsymbol{v})\boldsymbol{c}_{light}(\boldsymbol{n\cdot l_c})^+.\tag{10.1}
$$

区域光源对表面位置的照射有贡献的量是其辐射亮度($L_1$)和从该位置看到的尺寸($\omega_l$)的函数。正如我们在9.4节中看到的那样，点和方向光源是在实践中无法实现的近似值，因为它们的零立体角意味着无限的辐射。理解近似带来的视觉误差将有助于知道何时使用它，以及在不能使用它时采取的其他方法。这些误差取决于两个因素：光源的大小，从阴影点覆盖的立体角度，以及表面的光泽度。

图10.4显示了表面上的镜面高光尺寸和形状如何被材质粗糙度和光源尺寸影响。对于小光源，与视角相比，对着一个微小立体角的光源，误差很小。粗糙表面也倾向于显示光源尺寸小于抛光表面的效果。通常，朝向表面点的区域光发射和表面BRDF的镜面波瓣都是球面函数。如果我们考虑这两个函数的贡献是重要的方向集，我们获得两个立体角。误差的决定因素与发射角的相对大小与BRDF镜面高光立体角大小相比成比例。

最后，请注意区域光的高光可以通过使用点源光并增加表面粗糙度来近似。该观察结果对于获得对区域光积分的成本较低的近似是有用的。它还解释了为什么在实践中许多实时渲染系统仅使用点源光来产生合理的结果：艺术家可以弥补错误。然而，这样做是有害的，因为它将材质特性与特定的照明设置相结合。在改变照明场景时，以这种方式创建的内容看起来不正确。

对于特殊情况下的Lambertian表面，使用点光表示区域光可以是精确的。对于此类表面，出射辐射与辐照度成正比：

$$
L_o(\boldsymbol{v})=\frac{\rho_{ss}}{\pi}E,\tag{10.2}
$$

其中$ρ_{ss}$是次表面散射的反照率或漫反射颜色（第9.9.1节）。这种关系让我们使用等式10.1来计算辐照度更简单：

$$
E=\int_{\boldsymbol{l}\in\omega_l}L_l(\boldsymbol{n\cdot l})^+d\boldsymbol{l}\approx\pi\boldsymbol{c}_{light}(\boldsymbol{n}\cdot\boldsymbol{l}_c)^+.\tag{10.3}
$$

矢量辐照度的概念有助于理解在存在区域光源时辐照度如何表现。矢量辐照度由Gershun引入，他称之为光矢量，并由Arvo进一步扩展。使用矢量辐照度，可以将任意大小和形状的面光源精确地转换为点光源或定向光源。

想象一下，辐射 $L_i$ 的分布进入空间中的点p。见图10.5。我们现在假设 $L_i$ 是与波长无关的，因此可以表示为标量。对于以进入方向 $\boldsymbol{l}$ 为中心的每个无穷小立体角$d\boldsymbol{l}$ ，构造与 $\boldsymbol{l}$ 对齐并且具有等于从该方向进入的（标量）辐射的时间乘以 $d\boldsymbol{l}$ 的向量。最后，将所有这些矢量相加以产生矢量辐照度e：

$$
\boldsymbol{e}(\boldsymbol{p})=\int_{\boldsymbol{l}\in\Theta}L_i(\boldsymbol{p,l})\boldsymbol{l}d\boldsymbol{l},\tag{10.4}
$$

其中Θ表示在整个方向范围内执行积分。

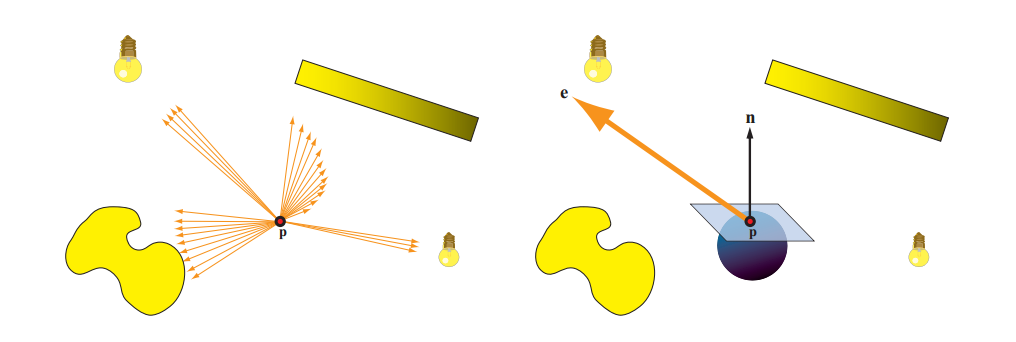
矢量辐照度e可用于通过执行点积来找到通过任何方向平面的p处的净辐照度：

$$
E(\boldsymbol{p,n})-E(\boldsymbol{p,-n})=\boldsymbol{n\cdot e(p)},\tag{10.5}
$$

其中n是平面的法线。通过平面的净辐照度(net irradiance)是流过平面的“正侧”（由平面法线n定义）和"负侧"的辐照度之间的差值。就其本身而言，净辐照度对着色没有用。但是，如果没有通过"负侧发射辐射"（换句话说，被分析的光分布没有l和n之间的角度超过90°的部分），则 $E(\boldsymbol{p,-n})=0$ 并且

$$
E(\boldsymbol{p,n})=\boldsymbol{n\cdot e(p)},\tag{10.6}
$$

单个区域光源的矢量辐照度可以与公式10.6一起用于照亮Lambertian表面与任何法线n，只要n与区域光源的任何部分相距不超过90°。见图10.6。

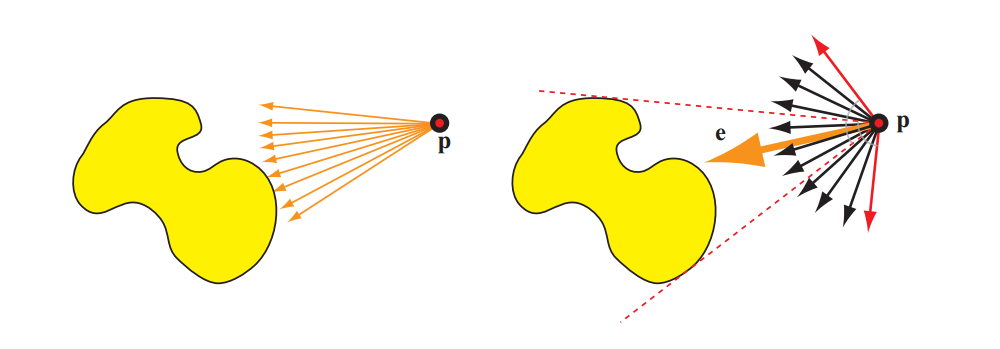
如果我们假设 $L_i$ 与波长无关，那么在一般情况下我们就不能再定义单个向量e。然而，彩色光通常在所有点处具有相同的相对光谱分布，这意味着我们可以将 $L_i$ 分解为颜色 $\boldsymbol{c}'$ 和与波长无关的辐射分布 $L'_i$ 。在这种情况下，我们可以计算 $\boldsymbol{e}$ 来表示 $L_i$ 并通过将 $\boldsymbol{n·e}$ 乘以 $c'$ 来扩展公式10.6。这样做会产生用于计算定向光源辐照度的相同方程式，具有以下替代：

$$
\begin{align}
\boldsymbol{l}_c&=\frac{\boldsymbol{e(p)}}{\Vert\boldsymbol{e(p)}\Vert},\\
\boldsymbol{c}_{light}&=\boldsymbol{c}'\frac{\Vert\boldsymbol{e(p)}\Vert}{\pi}.
\end{align}
\tag{10.7}
$$

我们已经有效地将任意形状和大小的面光源转换为定向光源而没有引入任何误差。

对于简单情况，可以解析地求解用于求出矢量辐照度的等式10.4。例如，想象一个球面光源，其中心为 $\boldsymbol{p}_l$ ，半径为 $r_l$ 。光从球体上的每个点向所有方向发射恒定的辐射亮度 $L_l$。对于这样的光源，方程10.4和10.7产生以下结果：

$$
\begin{align}
\boldsymbol{l}_c&=\frac{\boldsymbol{p}_l-\boldsymbol{p}}{\Vert\boldsymbol{p}_l-\boldsymbol{p}\Vert},\\
\boldsymbol{c}_{light}&=\frac{r_l^2}{\Vert\boldsymbol{p}_l-\boldsymbol{p}\Vert^2}L_l.
\end{align}
\tag{10.8}
$$

该等式与omni light（第5.2.2节）相同，其中 $c_{light_0} = L_l, r_0 = r_l$ ，以及标准的反平方距离衰减函数。可以调整该衰减函数以考虑球体内的点，并将光影响限制在给定的最大距离。有关此类调整的更多详细信息，请参见第5.2.2节。

所有这一切只有在没有“负面”辐照度的情况下才是正确的。考虑它的另一种方法是区域光源的任何部分都不能“在地平线下”，或被表面遮挡。我们可以概括这个陈述。对于朗伯曲面，区域和点光源之间的所有差异都是由遮挡差异引起的。来自点光源的辐照度遵守对于未被遮挡的所有法线的余弦定律。Snyder得出了球形光源的解析表达式，考虑了遮挡。这个表达非常复杂。然而，由于它仅依赖于两个量（$r/r_l$和 $θ_i$，$n$ 和 $l_c$ 之间的角度），因此可以将其预先计算为二维纹理。Snyder还提供了两个适用于实时渲染的函数近似值。

在图10.4中，我们看到区域照明的效果对粗糙表面不太明显。 这种观察结果还允许我们使用基于物理的较少但仍然有效的方法来模拟朗伯表面上的区域光的效果：包裹照明。 在这种技术中，对 $\boldsymbol{n·l}$ 的值进行了一些简单的修改，然后将其钳制为0。Forsyth给出了一种形式的包裹照明：

$$
E=\pi\boldsymbol{c}_{light}(\frac{(\boldsymbol{n\cdot l})+k_{wrap}}{1+k_{wrap}})^+,\tag{10.9}
$$

其中k环绕范围从0（对于点光源）到1（对于覆盖整个半球的区域光源）。Valve使用另一种模仿大面积光源效果的形式：

$$
E=\pi\boldsymbol{c}_{light}(\frac{(\boldsymbol{n\cdot l})+1}{2})^2,\tag{10.10}
$$

一般来说，如果我们计算区域照明，我们也应该修改我们的着色计算以考虑非点源光。如果我们不这样做，一些视觉效果可以被强烈的阴影消除。软阴影可能是区域光源最明显的效果，如第7章所述。

10.1.1 Glossy Materials

区域光对非朗伯表面的影响更为复杂。Snyder推导出球形光源的解决方案，但它仅限于原始的反射矢量Phong材料模型，并且非常复杂。在当今的实践中，需要近似值。

区域光在光泽表面上的主要视觉效果是亮点。见图10.4。它的大小和形状类似于区域光，而高光的边缘根据表面的粗糙度模糊。这一观察结果导致了几种经验近似的效应。这些在实践中可能非常有说服力。例如，我们可以修改突出显示计算的结果，以包含创建大平面突出显示区域的截止阈值。这可以有效地产生球形光的镜面反射错觉，如图10.7所示。

用于实时渲染的区域照明效果的大多数实际近似基于这样的想法：在每个着色点处找到将模仿非无限小光源的效果的等效点源照明设置。这种方法通常用于实时渲染以解决各种问题。这与我们在第9章中在表面的像素占位面积上处理BRDF积分时所见的原理相同。 它产生的近似值通常很cheap，因为所有工作都是通过改变着色方程的输入而不引入任何额外的复杂性来完成的。因为数学没有被改变，我们通常可以保证，在某些条件下，我们会回归到计算原始着色，从而保留其所有属性。 由于大多数典型系统的着色代码都基于点源光，因此区域光源使用这些代码只会引入本地的代码更改。

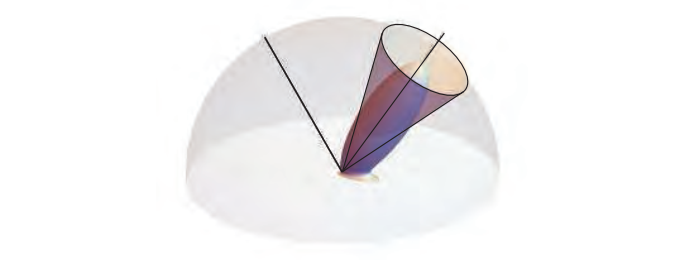
开发的第一个近似值是Mittring在虚幻引擎的“元素演示”中使用的粗糙度修改。想法是首先找到一个锥体，其中包含大部分光源辐照度到入射到表面的方向的半球上。然后我们拟合镜面周围类似的锥形，包含大多数的BRDF。见图10.8。然后，两个锥体都是半球上的函数的替身，并且它们包含这两个函数具有大于给定的任意截止阈值的方向的集合。这样做之后，我们可以通过找到一个具有不同粗糙度的新BRDF波瓣来近似光源和材料BRDF之间的卷积，该波瓣具有相应的锥体，其立体角等于光瓣角度和材质一的总和。

Karis展示了Mittring原理在GGX / Trowbridge-Reitz BRDF（第9.8.1节）和球面光源中的应用，导致GGX粗糙度参数 $α_g$ 的简单修改：

$$
\alpha_g'=(\alpha_g+\frac{r_l}{2\Vert\boldsymbol{p}_l-\boldsymbol{p}\Vert})^\mp
$$

请注意在1.2节中介绍的符号 $x^\mp$ 的使用，用于在0和1之间进行clamping。这种近似效果相当好并且非常便宜，但是对于有光泽的，几乎像镜子的材质而言会失败。发生这种失败是因为镜面波瓣总是光滑的并且不能模仿由区域光源在表面上的锐利反射引起的高光。此外，大多数microfacet BRDF模型的波瓣不是“紧凑的”（局部），但表现出较宽的衰减（镜面尾部），使粗糙度重新映射效果较差。见图10.9。

不是改变材料粗糙度，另一个想法是用光方向表示区域照明的光源，光方向根据被遮蔽的点而变化。这被称为最具代表性的点解决方案，修改光矢量，使其位于区域光表面上的点的方向上，该点朝向阴影表面产生最大的能量贡献。见图10.9。 Picott使用光线上的点来创建与反射光线最小的角度。卡里斯改进了Picott的公式，通过近似效率，最小角度点与球体上距反射光线最短距离的点。他还提出了一种廉价的配方，可以根据光线的强度进行测量，以保持整体发射的能量。见图10.10。大多数具有代表性的点解决方案都很方便，并且已针对各种光几何形状进行开发，因此了解它们的理论背景非常重要。这些方法类似于蒙特卡洛积分中的重要性采样的概念，其中我们通过对积分域上的样本求平均来数值计算定积分的值。为了更有效地这样做，我们可以尝试优先考虑对总体平均值有很大贡献的样本。

它们有效性的更严格证明在于定积分的中值定理（mean value theorem），它允许我们用同一函数的单个计算来代替函数的积分：

$$
\int_Df(x)dx=f(c)\int_D1.\tag{10.11}
$$

如果f(x)在D中是连续的，则 $\int_D1$ 是域的面积，点 $c\in D$ 位于D中函数minimum和maximum之间的线上。对于照明，我们考虑的积分是BRDF和被光线覆盖的半球区域的光辐照度。我们通常认为我们的光是均匀照射的，因此我们只需要考虑光衰减，并且大多数近似也假设域区域D从阴影点完全可见。即使有这些假设，确定点c和归一化因子 $\int_D1$ 仍然太昂贵，因此采用进一步的近似。

代表点解决方案也可以通过它们对突出显示形状的影响来构建。在表面的一部分上，由于反射矢量位于区域光所对应的方向锥之外，代表点不会发生变化，因此我们可以用点光进行有效照明。 然后，高光的形状仅取决于镜面凸起的底层形状。 或者，如果我们是反射矢量击中区域光的表面上的阴影点，则代表点将连续变化以指向最大贡献的方向。 这样做有效地扩展了镜面波瓣峰值，“扩大”它，这种效果类似于图10.7的硬阈值。

这个宽而恒定的高光峰值也是近似值中剩余的误差源之一。在较粗糙的表面上，区域光反射看起来比地面实况解决方案“更清晰”（即，通过蒙特卡洛积分获得）与粗糙度修改技术的过度模糊相反的视觉缺陷。为了解决这个问题，Iwanicki和Pesce开发了通过将BRDF波瓣，软阈值，代表点参数和比例因子（用于节能）拟合到通过数值积分计算的球面区域照明结果而获得的近似值。这些拟合函数产生一个参数表，该参数表由材料粗糙度，球半径以及光源中心与表面法线和视图矢量之间的角度索引。由于在着色器中直接使用这种多维查找表是昂贵的，因此提供了封闭形式的近似。最近，de Carpentier推出了一种改进的配方，以便在刨光角度更好地保持球形区域光源的高光形状，适用于基于微平面的BRDF。这种方法的工作原理是找到一个代表点，它使表面法线和光线半矢量之间的点积n·h最大化，而不是原始配方（源自Phong BRDF）的n·r。

10.1.2 General Light Shapes（常见的光源形状）

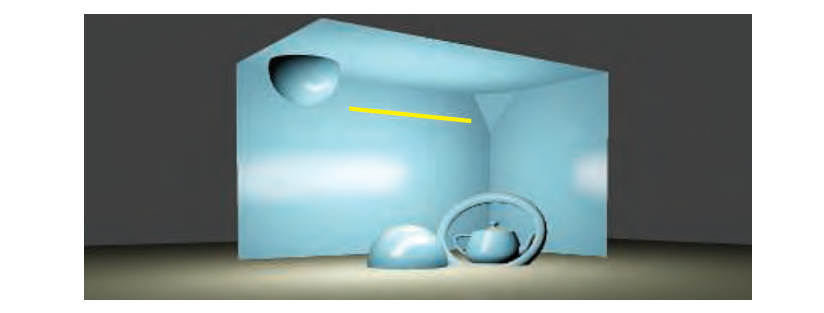
到目前为止，我们已经看到了一些通过均匀发射球面区域光和任意光泽BRDF来计算阴影的方法。 这些方法中的大多数采用各种近似，以便得到快速实时计算的数学公式，并且因此与问题的地面实况解决方案相比显示出不同程度的误差。然而，即使我们有计算能力来推导出精确解，我们仍然会犯一个大错误，我们将其嵌入到我们的照明模型的假设中。真实世界的灯通常不是球体，它们几乎不是完美的均匀发射体。见图10.11。球面区域的灯在实践中仍然很有用，因为它们提供了最简单的方法来打破点源光引入的照明和表面粗糙度之间的错误关联。然而，球形光源通常是大多数真实灯具的良好近似，只要它们相对较小。

由于基于物理的实时渲染的目标是生成令人信服的，合理的图像，所以只有到目前为止，我们才能通过将自己局限于理想化的场景来实现这一目标。这是计算机图形学中反复出现的权衡。我们通常可以选择生成准确的解决方案，以简化问题，简化假设，或者为更一般的问题推导近似解决方案，从而更紧密地模拟现实。

球形灯最简单的扩展之一是“管”灯（tube light，也称为“胶囊，capsules”），它可用于表示真实世界的荧光灯管。见图10.12。对于Lambertian BRDF，Picott显示了一个封闭形式的照明积分公式，相当于评估线性光线段极值处的两个点光源的照明，并具有适当的衰减函数：

$$
\int^{\boldsymbol{p}_1}_{\boldsymbol{p}_0}(\boldsymbol{n}\cdot\frac{x}{\Vert x\Vert})\frac{1}{\Vert x\Vert^2}dx=\frac{\frac{\boldsymbol{n\cdot p_o}}{\Vert\boldsymbol{p_0}\Vert^2}+\frac{\boldsymbol{n\cdot p_1}}{\Vert\boldsymbol{p_1}\Vert^2}}{\Vert\boldsymbol{p_0}\Vert\Vert\boldsymbol{p_1}\Vert+(\boldsymbol{p_0}\cdot\boldsymbol{p_1})},\tag{10.12}
$$

其中 $p_0$ 和 $p_1$ 是线性光的两个端点，n是表面法线。 Picott还推导出与Phong镜面BRDF积分的代表点解决方案，将其近似为放置在光线段上的点光源的光照，当连接到所考虑的表面点时，形成与该光点的最小角度。 反射向量。 该代表点解决方案将线性光动态地转换为点1，因此我们可以使用球形光的任何近似来将灯具“加厚”成胶囊。

与球形灯的情况一样，Karis通过使用与反射矢量的最小距离（而不是最小角度）的线上的点，在Picott的原始解决方案中呈现更有效（但稍微不那么准确）的变体，并呈现 一个缩放公式，试图恢复节能。

许多其他光形状的代表点近似可以相当容易地获得，例如环和Bézier段，但我们通常不希望我们的着色器分支太多。良好的光线形状可以用来代表我们场景中的许多真实世界的灯光。最具表现力的形状类别之一是平面区域光，其被定义为由给定几何形状约束的平面的一部分，例如矩形（在这种情况下它们也被称为卡片灯），盘，或更一般地，多边形。这些基元可用于广告牌和电视屏幕等发光面板，可用于常用的摄影照明（柔光箱，弹跳卡），模拟许多更复杂照明灯具的光圈，或代表从墙壁和其他场景中的大表面物体反射的照明。

Drobot推出了card light（以及disk）的第一个实用近似值。这又是一个代表性的点解决方案，但是由于将该方法扩展到平面的二维区域以及解决方案的整体方法的复杂性，这尤其值得注意。Drobot从均值定理开始，并且作为第一近似，确定用于光评估的良好候选点应该位于照明积分的全局最大值附近。

对于Lambert BRDF，这个积分是：

$$
L_l\int_{\boldsymbol{l}\in\omega_l}(\boldsymbol{n\cdot l})^+\frac1{r^2_\boldsymbol{l}}d\boldsymbol{l},\tag{10.13}
$$

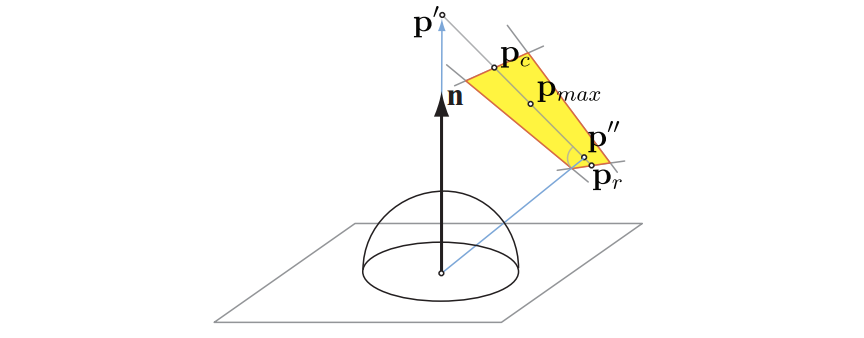
其中 $L_l$ 是由光发射的恒定辐射亮度，$\omega_l$ 是立体角，$r_l$ 是从 $l$ 方向到表面到光平面的光线的长度，$\boldsymbol{(n·l)}^+$ 是Lambertian 中的clamping。$\boldsymbol{(n·l)}^+$的最大值是光区域的边界上的点$p_c$，其最接近点 $p'$ ，$p'$ 通过使来自表面的光线在法线方向上与光平面相交而得到。类似地，最大值 $1/r^2$ 是最靠近点 $p''$ 的边界上的点 $\boldsymbol{p}_r$，该点在光平面上最接近被着色的表面点。见图10.13。然后，被积函数的全局最大值位于连接 $p_r$ 和 $p_c$ 的段上：$\boldsymbol{p}_{max} = t_m\boldsymbol{p}_c +(1-t_m)\boldsymbol{p}_r$，$t_m\in[0,1]$。Drobot使用数值积分来找到许多不同配置的最佳代表点，然后找到一个平均效果最好的单个$t_m$。

Drobot的最终解决方案采用了漫反射和高光照明的进一步近似，所有这些都是通过与数字上发现的地面实况解决方案进行比较来实现的。他还为纹理卡片灯的重要案例推导出一种算法，其中发射不被认为是恒定的，而是通过纹理在光的矩形区域上调制。使用三维查找表来执行该过程，该查找表包含在不同半径的圆形足迹上的发射纹理的预集成版本。Mittring采用类似的方法进行光泽反射，将反射光线与纹理矩形广告牌相交，并根据光线交叉距离索引预先计算的纹理模糊版本。这项工作先于Drobot的发展，但它是一种更经验，更少原则的方法，试图与地面实况完整解决方案相匹配。

对于平面多边形区域光的更一般情况，Lambert最初为完美漫射表面导出精确的闭合形式解。这种方法由Arvo改进，允许光滑材质建模为Phong镜面反射。Arvo通过将矢量辐照度的概念扩展到更高维度的辐照度张量并使用斯托克定理来解决区域积分作为沿着积分域的轮廓的更简单积分来实现这一点。他的方法所做的唯一假设是，从阴影表面点（通常可以通过用与表面相切的平面剪切光多边形来避开光）完全可见光，并且BRDF是径向对称的余弦。不幸的是，在实践中，Arvo的分析解决方案对于实时渲染而言非常昂贵，因为它需要根据区域光多边形的每个边缘评估其时间复杂度在所使用的Phong波瓣的指数中是线性的公式。最近，Lecocq通过找到轮廓积分函数的O(1)近似并将解扩展到一般的基于半矢量的BRDF，使这种方法更加实用。

到目前为止所描述的所有实际实时区域照明方法都采用某些简化假设以允许推导分析结构和近似来处理所得到的积分。 Heitz等人。采用线性变换余弦 linearly transformed cosines（LTCs，见https://eheitzresearch.wordpress.com/415-2/ ）的不同方法，产生实用，准确和通用的技术。他们的方法开始于在球体上设计一类具有高度表现力的功能（即，它们可以采用多种形状）并且可以容易地集成在任意球形多边形上。LTC仅使用由3×3矩阵转换的余弦波瓣，因此它们可以在半球上调整大小，拉伸和旋转以适应各种形状。一个简单的余弦叶（不像Blinn-Phong，不带指数）与球形多边形的积分已经很成熟，可追溯到兰伯特。 Heitz等人的关键观察结果。make是在叶片上用变换矩阵扩展积分不会改变其复杂性。我们可以通过矩阵的逆变换多边形域并取消积分内的矩阵，返回到简单的余弦作为被积函数。对于通用BRDF和区域光形状，剩下的唯一剩余工作是找到将球体上的BRDF函数表示为一个或多个LTC的方法（近似值），可以离线完成并在使用BRDF参数索引的查找数组中制表：粗糙度，入射角等。线性变换的基于余弦的解决方案既可用于一般纹理多边形区域光源，也可用于专门的，更便宜的计算形状，如卡片，磁盘和线光。LTC可能比代表点解决方案更昂贵，但更准确。

10.2 Environment Lighting（环境光照）

原则上，反射率（公式9.3）不区分直接来自光源的光和从天空散射的间接光或场景中的物体。 所有进入的方向都有辐射，反射方程对它们进行整合。然而，在实践中，直射光通常通过具有高辐射值的相对小的立体角来区分，并且间接光倾向于以中等到低的辐射值漫射地覆盖半球的其余部分。这种拆分提供了很好的实用理由来分别处理这两者。

到目前为止，区域光技术讨论了整合从光的形状发出的恒定辐射。这样做会为每个着色表面点创建一组具有恒定非零入射辐射的方向。我们现在研究的是在所有可能的传入方向上整合由变化函数定义的辐射的方法。见图10.16。

虽然我们一般会谈到间接和“环境”照明，但我们不打算研究全局照明算法。关键的区别在于，在本章中，所有着色数学都不依赖于场景中其他表面的信息，而是依赖于一小组光基元。因此，例如，虽然我们可以使用区域光来模拟墙壁上的光反射，这是一种全局效应，但着色算法不需要知道墙的存在。 它拥有的唯一信息是光源，所有阴影都是在本地执行的。全局照明（第11章）通常与本章的概念密切相关，因为许多解决方案可以被视为计算用于每个对象或表面位置的正确局部光基元集的方法，以模拟光在场景中来回反弹的相互作用。

环境光是最简单的环境照明模型，其中辐射不随方向变化并且具有恒定值 $L_A$。甚至这种环境照明的基本模型也显着改善了视觉质量。不考虑间接从物体反弹的光的场景看起来非常不现实。 在这样的场景中阴影中或背离光线的物体将是完全黑色的，这与现实中发现的任何场景不同。 第376页的图10.1中的moonscape接近，但即使在这样的场景中，一些间接光也会反射到附近的物体上。

环境光的确切影响取决于BRDF。对于朗伯曲面，固定辐射率 $L_A$ 导致对出射辐射的恒定贡献，无论表面法线n或视图方向$\boldsymbol{v}$ 如何：

$$
L_o(\boldsymbol{v})=\frac{\rho_{ss}}{\pi}L_A\int_{\boldsymbol{l}\in\Omega}(\boldsymbol{n\cdot l})d\boldsymbol{l}=\rho_{ss}L_A.\tag{10.14}
$$

在着色时，这种恒定的出射辐射贡献被添加到来自直接光源的贡献。对于任意BRDF，等效方程为：

$$
L_o(\boldsymbol{v})=L_A\int_{\boldsymbol{l}\in\Omega}f(\boldsymbol{l,v})(\boldsymbol{n\cdot l})d\boldsymbol{l}.\tag{10.15}
$$

该等式中的积分与方向反照率 $R(\boldsymbol{v})$ （9.3节中的公式9.9）相同，因此等式等于 $L_o(\boldsymbol{v})=L_AR(\boldsymbol{v})$。较旧的实时渲染应用程序有时假定 $R(\boldsymbol{v})$ 的常数值，称为环境颜色 $c_{amb}$。这进一步简化了 $L_o(\boldsymbol{v})= \boldsymbol{c}_{amb}L_A$的等式。

反射率方程忽略occlusion，即，将阻止许多表面点“看到”其他物体或同一物体的其他部分的一些进入方向。这种简化通常会降低真实感，但对于环境照明尤其明显，当忽略遮挡时，环境照明看起来非常平坦。解决这个问题的方法将在第11.3节中讨论，特别是在第11.3.4节中讨论。

10.3 Spherical and Hemispherical Functions（球面和半球函数）

为了将环境光照扩展到恒定项以外，我们需要一种方法来表示从任何方向到对象的入射辐射。首先，我们将辐射亮度视为仅是积分方向的函数，而不是表面位置。这样做是基于照明环境无限远的假设。

到达给定点的辐射对于每个进入的方向可以是不同的。照明可以从左边是红色，从右边是绿色，或者从顶部阻挡而不是从侧面阻挡。这些类型的量可以由球面函数（spherical functions）表示，球面函数在单位球体的表面上或在$\mathbb{R}^3$中的方向空间上定义。我们将此域称为$S$。这些函数如何工作不受它们是产生单个值还是多个值的影响。例如，用于存储标量函数的相同表示也可用于编码颜色值通，通过为每个颜色通道存储单独的标量函数。

假设朗伯表面，对于每个可能的表面法线方向，通过存储预先计算的辐照度函数（例如，与余弦波瓣卷积的辐射），可以使用球函数来计算环境光。更复杂的方法存储辐亮度并在运行时根据阴影表面点计算BRDF的积分。球面函数也广泛用于全局照明算法（第11章）。

与球形函数相关的是半球的函数，对于仅定义了一半方向的值的情况。例如，这些函数用于描述在没有来自下方的光的表面处的入射辐射。

我们将这些表示称为球形基础，因为它们是在球体上定义的函数的向量空间的基础。尽管环境/高光/方向形式（第10.3.3节）在技术上不是数学意义上的基础，但为简单起见，我们也将使用这些术语来引用它。将函数转换为给定表示称为投影（projection），并且从给定表示中计算函数的值称为重建（reconstruction）。

每个表示都有自己的权衡取舍。 我们可能在给定的基础上寻求的属性是：

• 高效的编码（投影）和解码（查找）。
• 使球函数表示为具有少量系数和低重建误差。
• 投影的旋转不变性是旋转函数的投影的结果，与旋转函数然后投影它相同。 这种等效意味着用例如球谐函数近似的函数在旋转时不会改变。
• 易于计算编码函数的总和和乘积。
• 易于计算球形积分和卷积。

10.3.1 Simple Tabulated Forms（简单的表格形式）

表示球形（或半球形）函数的最直接方法是选择多个方向并为每个方向存储一个值。 计算函数涉及在评估方向周围找到一些样本并用某种形式的插值重建该值。

这种表现形式简单而富有表现力。添加或乘以这些球形函数就像添加或乘以相应的列表条目一样简单。通过根据需要添加更多样本，我们可以编码具有任意低误差的许多不同球函数。

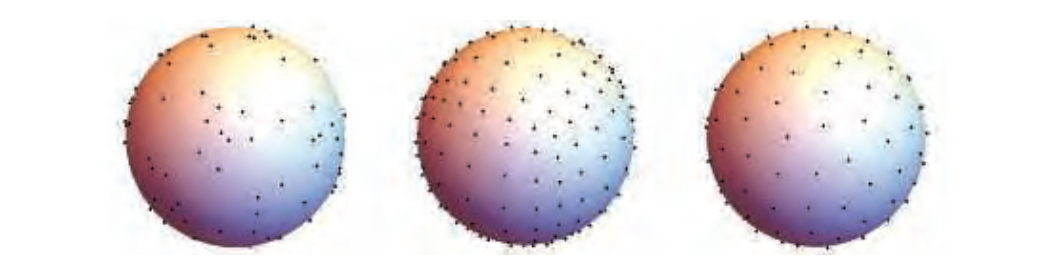
以一种允许有效检索的方式在一个球体上分布样本（见图10.17）并不是微不足道的，同时相对平等地表示所有方向。最常用的技术是首先将球体展开为矩形域，然后使用点网格对该域进行采样。由于二维纹理恰好表示矩形上的点（纹素）网格，我们可以使用纹素作为样本值的底层存储。这样做可以让我们利用GPU加速的双线性纹理过滤来快速查找（重建）。在本章的后面，我们将讨论环境贴图（第10.5节），它们是这种形式的球形函数，并讨论了解展开（unwrapping）球体的不同选项。

列表形式有缺点。在低分辨率下，硬件过滤提供的质量通常是不可接受的。计算卷积的计算复杂度是处理照明时的常见操作，与样本数量成正比，并且可能过高。此外，投影在旋转下不是不变的，这对于某些应用可能是有问题的。例如，想象一下当它撞击物体表面时编码从一组方向发出的光的辐射。如果对象旋转，则编码结果可能会以不同方式重建。这可能导致编码的辐射能量的变化，这可以表现为场景动画的脉动伪像。通过在投影和重建期间采用与每个样本相关联的精心构造的核函数，可以减轻这些问题。但更常见的是，仅使用足够密集的采样就足以掩盖这些问题。

通常，当我们需要存储复杂的高频函数时需要使用表格形式，这些函数需要以低误差编码许多数据点。如果我们需要紧凑地编码球形函数，只需要几个参数，就可以使用更复杂的基础。

环境立方体（AC）是一种流行的基础选择，是最简单的表格形式之一，由沿主轴定向的六个平方余弦瓣构成。它被称为环境“立方体”，因为它相当于将数据存储在立方体的面中，并在我们从一个方向移动到另一个方向时进行插值。对于任何给定方向，只有三个波瓣是相关的，因此不需要从内存中获取其他三个波瓣的参数。在数学上，环境立方体可以定义为：

$$
F_{AC}(\boldsymbol{d})=\boldsymbol{d}d\cdot sel_+(\boldsymbol{c}_+,\boldsymbol{c}_-,\boldsymbol{d}),\tag{10.16}
$$

其中 $\boldsymbol{c}_+$ 和 $\boldsymbol{c}_-$ 包含立方体面的六个值，而 $sel_+(\boldsymbol{c}_+,\boldsymbol{c}_-,\boldsymbol{d})$ 是一个向量函数，它为每个组件假定一个来自 $\boldsymbol{c}_+$ 或 $\boldsymbol{c}_-$ 的值，基于相应的组件 $\boldsymbol{d}$ 是否是正值。

环境立方体类似于立方体贴图（第10.4节），每个立方体面上都有一个纹素。在某些系统中，针对此特定情况在软件中执行重建可能比在立方体贴图上使用GPU的双线性过滤更快。斯隆推导出一种简单的公式，可以在环境立方体和球谐基础之间进行转换（第10.3.2节）。

使用环境立方体的重建质量相当低。 通过存储和插值八个值而不是六个值（对应于立方体顶点），可以获得稍微好一些的结果。 最近，Iwanicki和Sloan提出了另一种称为环境骰子（ambient dice ，AD）的方案。 基础由沿二十面体顶点定向的平方和四次幂余弦形成。存储的十二个值中有六个用于重建，并且确定检索哪六个的逻辑比环境立方体的相应逻辑稍微复杂一些，但结果的质量要高得多。

10.3.2 Spherical Bases（球面基础）

有许多方法可以将函数投影（编码）到使用固定数量的值（系数）的表示中。我们所需要的只是一个数学表达式，它跨越我们的球形域，我们可以改变一些参数。然后，我们可以通过拟合来近似我们想要的任何给定函数，即，找到最小化我们的表达式和给定函数之间的误差的参数的值。

最小的可能选择是使用常量：

$$
F_c(\theta,\phi)=c\cdot1.
$$

我们可以通过在单位球的表面积上对其求平均来推导给定函数f的投影：$c =\frac1{4π}\int_Ωf(θ,\phi)$。周期函数的平均值c也称为$DC$分量。这个基具有简单的优点，甚至尊重我们正在寻找的一些属性（易于重建，添加，产品，旋转不变性）。然而，它不能很好地表达大多数球函数，因为它只是用它们的平均值代替它们。我们可以使用两个系数a和b构造一个稍微复杂的近似：

$$
F_{hemi}(\theta,\phi)=a+\frac{\cos(\theta)+1}2(b-a),
$$

它创建了一个可以在极点处编码精确值的表示，并且可以在球体表面之间进行插值。这种选择更具表现力，但现在投影更复杂，并且对于所有旋转都不是不变的。事实上，这个基础可以看作是一个表格形式，只有两个样本，放在两极。

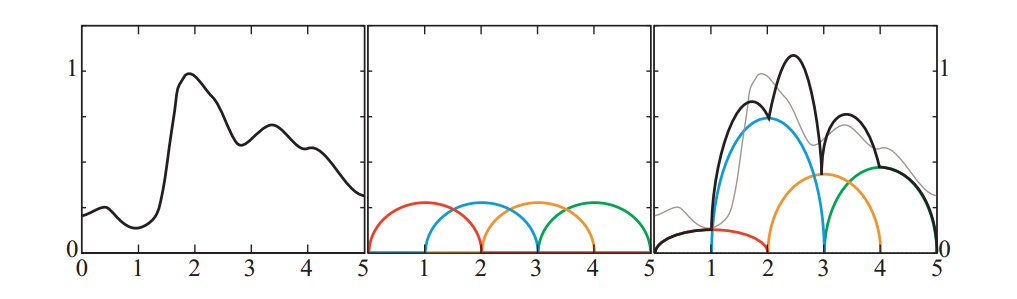
通常，当我们讨论函数空间的基础时，我们意味着我们有一组函数，其线性组合（加权和求和）可用于表示给定域上的其他函数。 这个概念的一个例子如图10.18所示。 本节的其余部分探讨了可用于近似球体上的函数的一些基础选择。

Spherical Radial Basis Functions

使用GPU硬件过滤的表格形式的低质量重建至少在某种程度上是由用于内插样本的双线性形状函数引起的。其他功能可用于对样本进行加权以进行重建。这些功能可以产生比双线性滤波更高质量的结果，并且它们可以具有其他优点。通常用于此目的的一类功能是球形径向基函数（spherical radial basis functions，SRBF）。它们是径向对称的，这使得它们仅具有一个参数的功能，即它们所朝向的轴与评估方向之间的角度。该基础由一组称为波瓣（lobes）的这样的函数形成，这些函数遍布球体。函数的表示由每个波瓣的一组参数组成。这个集合可以包括它们的方向，但它使投影更加困难（需要非线性，全局优化）。由于这个原因，通常假定波瓣方向是固定的，在球体上均匀分布，并且使用其他参数，例如每个波瓣的大小或其扩展，即所覆盖的角度。通过计算给定方向的所有波瓣并对结果求和来执行重建。

Spherical Gaussians

SRBF波瓣的一个特别常见的选择是球面高斯（SG），在方向统计中也称为von Mises-Fisher分布。我们应该注意到von-Mises-Fisher分布通常包括归一化常数，我们在公式中避免使用。单个lobe可以定义为：

$$
G(\boldsymbol{v,d},\lambda)=e^{\lambda(\boldsymbol{v\cdot d}-1)},\tag{10.17}
$$

其中v是计算方向（单位矢量），d是波瓣方向轴（分布的平均值，也是归一化的），λ≥0是波瓣锐度（控制其角宽度，也称为concentration parameter或spread）。

为了构造球面基，我们使用给定数量的球面高斯的线性组合：

$$
F_G(\boldsymbol{v})=\sum_kw_kG(\boldsymbol{v,d_k},\lambda_k).\tag{10.18}
$$

将球函数投影到该表示中需要找到参数集 ${w_k,\boldsymbol{d}_k,\lambda_k }$ 最小化重建误差。该过程通常通过数值优化来完成，通常使用非线性最小二乘法优化算法（例如Levenberg-Marquardt）。请注意，如果我们允许完整集参数在优化过程中发生变化，我们就不会使用函数的线性组合，因此公式10.18不代表基础。只有当我们选择一组固定的lobe（方向和点差）时才能获得适当的基础，以便整个域被很好地覆盖，并通过仅拟合权重 $w_k$ 来执行投影。这样做也极大地简化了优化问题，因为现在可以将其表述为普通最小二乘优化。如果我们需要在不同的数据集（投影函数）之间进行插值，这也是一个很好的解决方案。对于该用例，允许波瓣方向和锐度变化是有害的，因为这些参数是高度非线性的。

这种表示的优势在于 $SGs$ 上的许多操作都具有简单的解析形式。两个球面高斯的乘积是另一个球面高斯：

$$
G_1G_2=G(\boldsymbol{v},\frac{\boldsymbol{d}'}{\Vert\boldsymbol{d}'\Vert},\lambda'),
$$

where:

$$
\boldsymbol{d}'=\frac{\lambda_1\boldsymbol{d}_1+\lambda_2\boldsymbol{d}_2}{\lambda_1+\lambda_2},;;\lambda'=(\lambda_1+\lambda_2)\Vert\boldsymbol{d}'\Vert.
$$

球体高斯在球体上的积分也可以通过分析计算：

$$
\int_\Omega G(\boldsymbol{v})d\boldsymbol{v}=2\pi\frac{1-e^{2\lambda}}{\lambda},
$$

这意味着两个球面高斯相乘的积分也有一个简单形式的公式。

如果我们可以将光辐射表示为球面高斯，那么我们可以将其乘积与以相同表示编码的BRDF集成以执行照明计算。 由于这些原因，SGs已被用于许多研究项目以及工业应用。

至于平面上的高斯分布，可以推广von Mises-Fisher分布以允许各向异性。徐等人。引入了各向异性球面高斯（ASGs, 见图10.19），它是通过用两个补充轴t和b增加单向d来定义的，它们共同形成一个正交切线框架：

$$
G(\boldsymbol{v},[\boldsymbol{d,t,b}],[\lambda,\mu])=S(\boldsymbol{v,d})e^{-\lambda(\boldsymbol{v\cdot t})^2-\mu(\boldsymbol{v\cdot b})^2},\tag{10.19}
$$

其中λ, μ≥0控制沿切线框的两个轴的波瓣扩散，$S(v,d)=(v·d)^+$是平滑项。 这个项是定向统计中使用的Fisher-Bingham分布与我们用于计算机图形的ASG之间的主要区别。 徐等人。 还为积分，乘积和卷积运算符提供分析近似。

虽然SG具有许多理想的属性，但它们的一个缺点是，与表格形式不同，并且在一般内核（带宽）有限的情况下，它们具有全局支持。每个波瓣对于整个球体都是非零的，即使其衰减相当快。 这个全局范围意味着如果我们使用N个lobe来表示一个函数，我们将需要它们中的所有N个用于任何方向的重建。

Spherical Harmonics（球谐波）

球谐函数（SH）是球面上的一组正交基函数。正交基函数集是一组，使得来自该集的任何两个不同函数的内积为零。内积是点乘的更一般但相似的概念。两个向量的内积是它们的点积：分量对之间的乘积之和。通过考虑这些函数的积分，我们可以类似地推导出两个函数的内积的定义：

$$
\langle f_i(x),f_j(x) \rangle \equiv \int f_i(x)f_j(x)dx,\tag{10.20}
$$

积分在相关域上执行的。对于图10.18中所示的函数，相关域在x轴上介于0和5之间（请注意，此特定函数集不是正交的）。对于球形函数，形式略有不同，但基本概念是相同的：

$$
\langle f_i(\boldsymbol{n}),f_j(\boldsymbol{n}) \rangle \equiv \int_{\boldsymbol{n}\in\Theta} f_i(\boldsymbol{n})f_j(\boldsymbol{n})d\boldsymbol{n},\tag{10.21}
$$

其中 $\boldsymbol{n}\in\Theta$ 表示在单位球上执行积分。

标准正交集(orthonormal set)是一个正交集（orthogonal set），即集合中任何函数和它自身的内积等于1。更正式地说，函数集 $f_j()$是otrhonormal的条件是：

$$
\langle f_i(),f_j() \rangle =
\begin{cases}
0, ;where ;i\ne j,\\
1, ;where ;i= j.
\end{cases}
\tag{10.22}
$$

图10.20显示了一个类似于图10.18的示例，其中基函数是标准正交的。 注意，图10.20中所示的标准正交基函数不重叠。 这种情况对于非负函数的标准正交集是必要的，因为任何重叠都意味着非零内积。 在其范围的一部分上具有负值的函数可以重叠并且仍然形成正交集。 这种重叠通常导致更好的近似，因为它允许碱基是平滑的。 具有不相交域的基础往往会导致不连续。

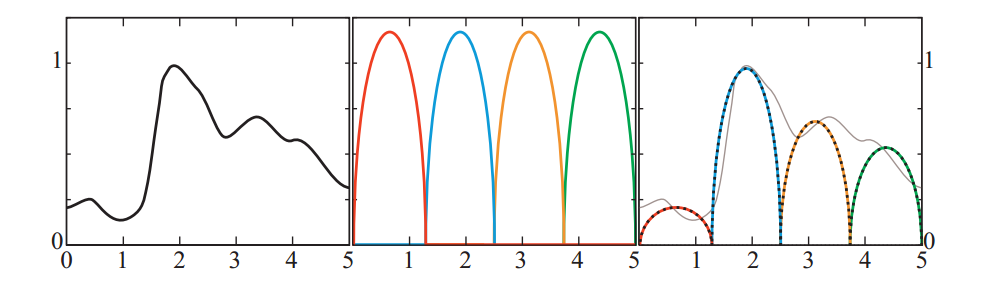
标准正交基的优点是找到与目标函数最接近的近似的过程是直截了当的。为了执行投影，每个基函数的系数是目标函数 $f_{target}()$ (具有适当的基函数)的内积：

$$
k_j=\langle f_{target}(x),f_j(x) \rangle,\\
f_{target}(x)\approx\sum_{j=1}^nk_jf_j().\tag{10.23}
$$

在实践中，该积分必须通过数值计算，通常通过蒙特卡罗采样，平均在球体上均匀分布的n个方向。

正交基础在概念上类似于对于三维向量的“标准基”。标准基的目标不是函数，而是一个点的位置。标准基由三个向量组成（每个向量一个） 通过公式10.22中使用的相同定义的标准基。标准基上的点投影的方法也是相同的，因为系数是位置之间的点积的结果。维度）而不是一组函数。 矢量和基矢量。一个重要的区别是标准基准精确地再现每个点，而有限的基函数集只能近似其目标函数。结果可以是精确的，因为标准基础使用三个基矢量来表示三个 - 维空间。函数空间具有无限多个维度，因此有限数量的基函数永远无法完美地表示它。

球谐波是正交的和标准正交的，并且它们具有其他几个优点。 它们是旋转不变的，并且SH基函数的评估成本低廉。它们是单位长度矢量的x，y和z坐标中的简单多项式。然而，像球形高斯一样，它们具有全局支持，因此在重建期间需要计算所有基函数。基函数的表达式可以在几个参考文献中找到，包括斯隆的演示文稿。他的演讲值得注意，因为它讨论了许多处理球谐函数的实用技巧，包括公式和某些情况下的着色器代码。最近，斯隆还推出了有效的SH重建方法。

SH基函数排列在频带中。第一个基函数是常数，接下来的三个是在球体上缓慢变化的线性函数，接下来的五个函数表示稍微更快变化的二次函数。见图10.21。低频率（即在球体上缓慢变化）的函数，例如辐照度值，用相对较少数量的SH系数精确表示（我们将在第10.6.1节中看到）。

当投射到球谐函数时，得到的系数表示投影函数的各种频率的幅度，即其频谱。在该谱域中，基本性质成立：两个函数的乘积的积分等于函数投影的系数的点积。此属性允许我们有效地计算光照积分。

关于球谐函数的许多操作在概念上是简单的，沸腾到系数向量上的矩阵变换。在这些操作中，重要的是计算两个函数的乘积投射到球谐函数，旋转投影函数，计算卷积。在实践中SH中的矩阵变换意味着这些操作的复杂性在所使用的系数的数量上是二次的，这可能是相当大的成本。幸运的是，这些矩阵通常具有可以被利用来设计更快算法的特殊结构。Kautz等人提出了一种通过将旋转计算分解为围绕x轴和z轴的旋转来优化旋转计算的方法。 Hable给出了一种用于快速旋转低阶SH投影的流行方法。Green的调查讨论了如何利用旋转矩阵的块结构来加快计算速度。目前，现有技术的特点是分解为纬向谐波，如Nowrouzezahrai等人所提出的。

如下所述的光谱变换（例如球谐波和H-basis）的常见问题是它们可以表现出称为振铃的视觉伪像（也称为吉布斯现象）。如果原始信号包含无法用带限近似表示的快速变化，则重建将显示振荡。在极端情况下，这种重建功能甚至可以产生负值。可以使用各种预过滤方法来解决该问题。
$$

$$

Other Spherical Representations

许多其他表示可以使用有限数量的系数来编码球面函数。线性变换后的余弦（第10.1.2节）是能够有效逼近BRDF函数的表示的一个例子，同时具有易于在球体的多边形截面上可积的特性。

球面小波是平衡空间中的局部性（具有紧凑支撑）和频率（平滑性）的基础，允许压缩表示高频功能。球形分段常数基函数将球体划分为具有恒定值的区域，并且依赖于矩阵因子分解的双聚类近似也已用于环境照明。

10.3.3 Hemispherical Bases

尽管上述基础可用于表示半球函数，但它们是浪费的。 信号的一半总是等于零。在这些情况下，通常优选使用直接在半球形域上构建的表示。这与在曲面上定义的函数尤其相关：BRDF，入射辐射和到达对象的给定点的辐照度都是常见的例子。这些函数自然地受限于以给定表面点为中心并与表面法线对齐的半球; 它们没有指向对象内部的方向的值。

Ambient/Highlight/Direction

沿着这些线的最简单的表示之一是一个恒定函数和一个方向的组合，其中信号在半球上最强。它通常被称为环境/高光/方向（Ambient/Highlight/Direction，AHD）基础，其最常见的用途是存储辐照度。名称AHD表示各个组件代表的含义：恒定的环境光，加上单个方向光，近似于“高亮”方向的辐照度，以及大部分入射光聚集的方向。AHD基础通常需要存储8个参数。方向矢量使用两个角度，环境和定向光强度使用两种RGB颜色。第一个值得注意的用途是在Quake III游戏中，动态物体的体积照明以这种方式存储。从那时起用于几个称号，例如“使命召唤”franchise。

以这种表示的投射有点棘手。 因为它是非线性的，所以找到接近给定输入的最佳参数在计算上是昂贵的。在实践中，使用启发式方法代替。信号首先投射到球谐波，最佳线性方向用于定向余弦波瓣。给定方向，可以使用minimalsquares最小化来计算环境和高光值。 Iwanicki和Sloan展示了如何在执行非负性的同时执行此投影。

Radiosity Normal Mapping/Half-Life 2 Basis

Hemispherical Harmonics/H-Basis

hemispherical harmonics (HSHs) ...暂略

10.4 Environment Mapping

在一个或多个图像中记录球形函数称为环境映射，因为我们通常使用纹理映射来实现表中的查找。这种表现形式是最强大和最受欢迎的环境照明形式之一。与其他球形表示相比，它消耗更多内存，但实时解码简单快速。此外，它可以表示任意高频率的球形信号（通过增加纹理的分辨率）并准确地捕获任何环境辐射范围（通过增加每个通道的位数）。这样的准确性是有代价的。 与存储在其他常用纹理中的颜色和着色器属性不同，存储在环境贴图中的辐射值通常具有高动态范围。每个纹素的位数越多意味着环境贴图比其他纹理占用更多的空间，并且访问速度可能更慢。

我们对任何全局球函数（即，用于场景中的所有对象的函数）具有基本假设，即入射辐射 $L_i$ 仅取决于方向。这种假设要求被反射的物体和光线很远，反射器不会反射自身。

依赖于环境映射的着色技术通常不具有表示环境照明的能力，而在于我们如何将它们与给定材料集成。也就是说，为了进行整合，我们必须在BRDF上使用哪种近似和假设？反射映射是环境映射的最基本情况，我们假设BRDF是一个完美的镜像。光学平坦的表面或镜子将入射光线反射到光的反射方向 $r_i$（第9.5节）。类似地，输出辐射亮度包括来自仅一个方向的入射辐射，即反射视图矢量 r。该向量的计算方式与 $r_i$ 相同（公式9.15）：

$$
\boldsymbol{r}=2(\boldsymbol{n\cdot v})\boldsymbol{n}-\boldsymbol{v}.\tag{10.28}
$$

对于镜像的反射方程大大简化：

$$
L_o(\boldsymbol{v})=F(\boldsymbol{n,r})L_i(\boldsymbol{r}),\tag{10.29}
$$

其中F是菲涅耳项（第9.5节）。请注意，与基于半矢量的BRDF（使用半矢量h和l或v之间的角度）中的菲涅耳项不同，公式10.29中的菲涅耳项使用表面法线n和反射矢量r之间的角度（这与n和v之间的角度相同）。

由于入射辐射 $L_i$ 仅取决于方向，因此可以将其存储在二维表中。这种表示使我们能够有效地照亮具有任意入射辐射分布的任何形状的镜面状表面。我们通过为每个点计算r并在表中查找辐射来实现。该表称为environment map，由Blinn和Newell介绍。见图10.23。

reflection mapping 算法的步骤如下：

• 生成/加载表示环境的纹理。
• 对于每个包含反射对象的像素，计算该对象表面位置的法线。
• 从v和n计算reflected view vector 。
• 使用reflected view vector 计算环境贴图中的索引，该索引表示反射视图方向上的入射辐射。
• 使用环境贴图中的纹素数据作为公式10.29中的入射辐射。

值得一提的环境映射的潜在问题是。使用环境映射时，比较平的面通常不能很好地工作。平坦表面的问题是从其反射的光线通常不会变化超过几度。这种紧密的聚类导致环境表的一小部分被映射到相对较大的表面上。在第11.6.1节中讨论的也使用发射辐射的位置信息的技术可以提供更好的结果。此外，如果我们假设完全平坦的表面，例如地板，则可以使用平面反射的实时技术（第11.6.2节）。

用纹理数据照亮场景的想法也称为基于图像的照明（image-based lighting，IBL），通常当使用捕获360度全景时，HDR图像的相机从真实世界场景获得环境地图。

有多种投影函数可将反射的视图矢量映射到一个或多个纹理中。我们在这里讨论比较流行的映射，并注意每个映射的优势。

10.4.1 Latitude-Longitude Mapping

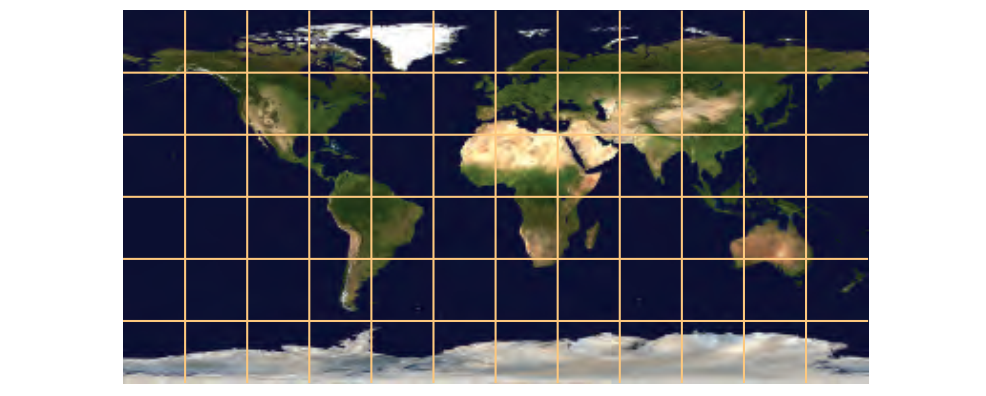
1976年，Blinn和Newell开发了第一个环境映射算法。他们使用的映射是在地球上使用的熟悉的纬度/经度系统，这就是为什么这种技术通常被称为纬度 - 经度映射或纬度 - 长度映射的原因。他们的计划不像是从外面看的地球，而是像夜空中的星座图。 就像地球上的信息可以展平为墨卡托或其他投影地图一样，可以将围绕空间中的点的环境映射到纹理。 当针对特定表面位置计算反射视图矢量时，矢量被转换为球面坐标 $(ρ,\phi)$ 。这里的φ，相当于经度，从0到2π弧度变化，ρ，纬度，从0到π弧度变化。 对 $(ρ,\phi)$ 由公式10.30计算，其中 $\boldsymbol{r} =(\boldsymbol{r}_x, \boldsymbol{r}_y, \boldsymbol{r}_z)$ 是归一化的反射视图向量，其中+ z为上方向：

$$
\rho=arccos(r_z);and;\phi=atan2(r_y,r_x).\tag{10.30}
$$

有关atan2的说明，请参见第一章。然后，这些值用于访问环境贴图并检索在反射视图方向上看到的颜色。请注意，纬度 - 经度映射与Mercator projection不同。它使纬度线之间的距离保持恒定，而Mercator在极点处变为无穷大。

将球体展开到平面中总是需要一些变形，特别是如果我们不允许多次切割，并且每个投影在保留区域，距离和局部角度之间都有自己的权衡。 这种映射的一个问题是信息密度远不一致。 从图10.25的顶部和底部的极端拉伸可以看出，极点附近的区域比赤道附近的区域接收更多的纹素。 这种失真是有问题的，不仅因为它不会导致最有效的编码，而且在采用硬件纹理滤波时也会导致伪像，特别是在两极奇点处可见。 滤波内核不遵循纹理的拉伸，因此在具有较高纹理像素密度的区域中有效地收缩。 还要注意，尽管投影数学很简单，但它可能效率不高，因为诸如反余弦的超越函数在GPU上是昂贵的。

10.4.2 Sphere Mapping

最初由威廉姆斯提及，由米勒和霍夫曼独立开发，球体映射是一般商业图形硬件支持的第一种环境贴图技术。纹理图像是从完全反射的球体中正交观察的环境外观得出的，因此这种纹理称为球体图。制作真实环境的球体地图的一种方法是拍摄闪亮球体的照片，例如圣诞树装饰物。 见图10.26。

得到的圆形图像也称为光探测器，因为它捕获球体位置处的照明情况。即使我们在运行时使用其他编码，拍摄球形探针也是捕获基于图像的照明的有效方法。如果捕获具有足够的分辨率来克服方法之间的失真差异，我们总是可以在球形投影和另一种形式之间进行转换，例如稍后讨论的立方体映射（第10.4.3节）。

反射球体在整个球体的正面显示整个环境。它将每个反射的视图方向映射到该球体的二维图像上的点。假设我们想要转向另一个方向，即在球体地图上给出一个点，我们会想要反射的视图方向。为此，我们将在该点处取球面上的曲面法线，然后生成反射的视图方向。因此，为了反转过程并从反射的视图矢量获取球体上的位置，我们需要在球体上导出曲面法线，然后生成访问球体贴图所需的$(u, v)$参数。

球体的法线是反射视图矢量r和原始视图矢量v之间的半角矢量，它是球体图的空间中的(0,0,1)。见图10.27。该法向量n是原始和反射视图矢量的总和，即 $(r_x, r_y, r_z + 1)​$。归一化此向量会使单位正常：

$$
\boldsymbol{n}=(\frac{r_x}m,\frac{r_y}m,\frac{r_z+1}m),;where;m=\sqrt{r_x^2+r_y^2+(r_z + 1)^2}.\tag{10.31}
$$

如果球体位于原点并且其半径为1，则单位法线的坐标也是球体上法线的位置h。我们不需要 $h_z$，因为（hx，hy）描述了球体图像上的一个点，每个值都在[-1,1]范围内。要将此坐标映射到范围[0,1）以访问球体贴图，请将每个坐标除以2并添加一半：

$$
m=\sqrt{r_x^2+r_y^2+(r_z + 1)^2},;u=\frac{r_x}{2m}+0.5,;and;v=\frac{r_y}{2m}+0.5.\tag{10.32}
$$

与纬度 - 经度映射相比，球体映射计算起来更简单，并且显示了位于图像圆边缘周围的一个奇点。缺点是球体贴图纹理捕获仅对单个视图方向有效的环境视图。此纹理确实捕获整个环境，因此可以计算新查看方向的纹理坐标。然而，这样做会导致视觉伪影，因为球形图的小部分由于新视图而变得放大，并且边缘周围的奇点变得明显。在实践中，球形图通常被假定为跟随相机，在视图空间中操作。

由于球面图是针对固定视图方向定义的，因此原则上球面图上的每个点不仅定义反射方向，还定义表面法线。见图10.27。对于任意各向同性BRDF，可以求解反射方程，并且其结果可以存储在球形图中。该BRDF可包括漫反射，镜面反射，逆反射和其他项。只要照明和视图方向固定，球形图就是正确的。甚至可以使用在实际照射下的真实球体的摄影图像，只要球体的BRDF是均匀的和各向同性的。

也可以索引两个球面图，一个具有反射矢量，另一个具有曲面法线，以模拟镜面反射和漫反射环境效果。 如果我们调整存储在球体贴图中的值以考虑表面材料的颜色和粗糙度，我们有一种廉价的技术可以产生令人信服的（尽管与视图无关的）材料效果。 这种方法由雕刻软件Pixologic ZBrush推广为“MatCap”着色。见图10.28。

10.4.3 Cube Mapping

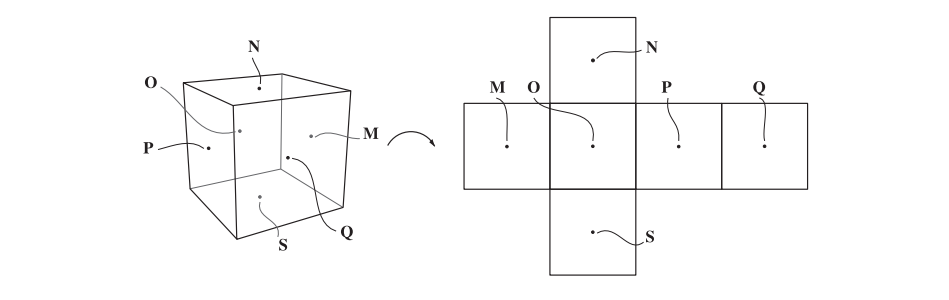
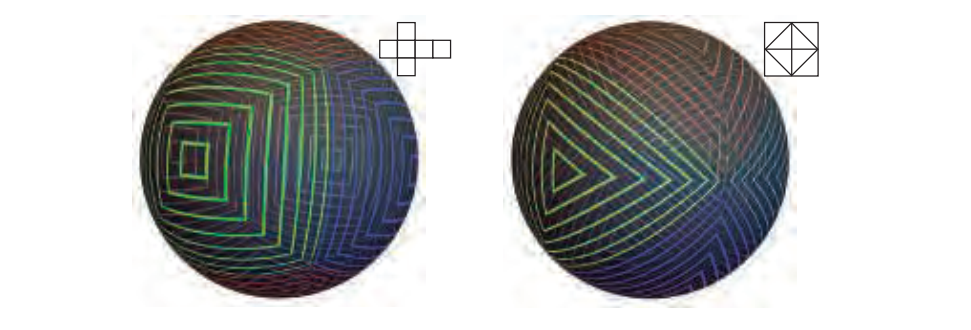
1986年，Greene推出了立方体环境地图，通常称为立方体地图。 这种方法是当今最流行的方法，其投影直接在现代GPU上的硬件中实现。 通过将环境投影到立方体的侧面来创建立方体贴图，该立方体的中心位于相机的位置。 然后将立方体面上的图像用作环境贴图。 立方体贴图通常在“交叉”图中可视化，即打开立方体并将其展平到平面上。但是，在硬件立方体贴图上存储为六个方形纹理，而不是单个矩形纹理，因此不会浪费空间。

通过在立方体中心使用相机渲染场景六次，以90°视角观察每个立方体面，可以合成地创建立方体贴图。见图10.31。为了从真实环境生成立方体贴图，通常通过拼接或专用相机获取的球形全景图被投影到立方体贴图坐标系中。

与球体映射不同，立方体环境映射与视图无关（view-independent）。它还具有比纬度 - 经度映射更加均匀的采样特性，纬度 - 经度映射与赤道相比对极点进行过采样。Wan等人提出了一种称为 $isocube$ 的映射，它具有比立方体映射更低的采样率差异，同时仍然利用立方体映射纹理硬件来提高性能。

访问立方体贴图非常简单。任何矢量都可以直接用作三分量纹理坐标，以便在指向的方向上获取数据。因此，对于反射，我们可以将反射的视图矢量r传递给GPU，甚至不需要对其进行标准化。在较旧的GPU上，双线性过滤可以显示沿立方体边缘的接缝，因为纹理硬件无法在不同的立方体面上正确过滤（执行起来有些昂贵的操作）。开发了回避这个问题的技术，例如使视图投影更宽一些，以便单个面也包含这些相邻的纹素。所有现代GPU现在都可以跨边缘正确执行此过滤，因此不再需要这些方法。

10.4.4 Other Projections

今天，立方体贴图是环境照明最受欢迎的表格表示，因为它具有多功能性，再现高频细节的准确性以及GPU上的执行速度。 但是，已经开发了一些值得一提的其他投影。

Heidrich和Seidel建议使用两个纹理来执行双抛物面环境映射（dual paraboloid environment mapping）。这个想法就像是球体映射的想法，但不是通过记录球体环境的反射来生成纹理，而是使用两个抛物线投影。每个抛物面创建一个类似于球体地图的圆形纹理，每个抛物面覆盖一个环境半球。

与球体映射一样，反射的视图光线在地图的基础上，即在其参照系中计算。反射视图矢量的z分量的符号用于决定要访问的两个纹理中的哪一个。访问函数是

$$
u=\frac{r_x}{2(1+r_z)}+0.5,;v=\frac{r_y}{2(1+r_z)}+0.5\tag{10.33}
$$

对于正面图像，对于背面图像，对于 $r_z$ 具有符号反转。

与球形图相比，抛物线图具有更均匀的纹理像素采样，甚至是立方体图。但是，必须注意在两个投影之间的接缝处进行适当的采样和插值，这使得访问双抛物面图更加昂贵。

八面体映射（Octahedral mapping）是另一个值得注意的投影。它不是将周围的球体映射到立方体，而是映射到八面体（见图10.32）。为了将这种几何形状展平成纹理，将其八个三角形面切割并布置在平面上。可以是正方形或矩形配置。如果我们使用方形配置，访问八面体映射的数学非常有效。 给定反射方向r，我们使用绝对值 $L_1$ 计算标准化版本：

$$
\boldsymbol{r'}=\frac{\boldsymbol{r}}{\vert r_x\vert+\vert r_y\vert+\vert r_z\vert}.
$$

对于 $r'_y​$ 为正的情况，我们可以将方形纹理索引为：

$$
u=r_x'\cdot0.5+0.5,v=r_y'\cdot0.5+0.5.\tag{10.34}
$$

在 $r'_y$ 为负的情况下，我们需要用变换将“八面体的后半部分”向外折叠

$$
u=(1-\vert r'_z\vert)\cdot sign(r_x')\cdot0.5+0.5,;v=(1-\vert r_x'\vert)\cdot sign(r'_z)\cdot0.5+0.5.\tag{10.35}
$$

八面体映射不会受到双抛物面映射的滤波问题的影响，因为参数化的接缝对应于所使用的纹理的边缘。纹理“环绕”采样模式可以自动从另一侧访问纹素并执行正确的插值。虽然投影的数学稍微涉及，但实际上性能更好。引入的失真量类似于立方体的数量当不存在立方体贴图纹理硬件时，八面体贴图可能是一个很好的选择。另一个值得注意的用途是仅使用两个坐标表示三维方向（标准化向量），作为压缩（第16.6节）。

对于围绕轴径向对称的环境地图的特殊情况，Stone提出了使用单个一维纹理的简单因子分解，该纹理沿着来自对称轴的任何子午线存储辐射值。 他将这个方案扩展到二维纹理，在每一行中存储一个预先与不同的Phong波瓣卷积的环境地图。 这种编码可以模拟各种材料，并用于编码晴朗天空发出的辐射。

10.5 Specular Image-Based Lighting

虽然环境贴图最初是作为渲染镜像表面的技术而开发的，但它也可以扩展为光泽反射。当用于模拟无限远光源的一般镜面反射效果时，环境贴图也称为镜面光探测器。使用该术语是因为它们捕获场景中给定点处的所有方向的辐射（因此探测），并且使用该信息来评估一般BRDF，不仅是纯镜子或朗伯曲面的受限情况。名称specular cube maps 也用于将环境光照存储在立方体贴图中的常见情况，这些立方体贴图已被操纵以模拟光泽材质上的反射。

为了模拟表面粗糙度，可以对纹理中的环境表示进行预滤波。通过模糊环境贴图纹理，我们可以呈现镜面反射，看起来比完全镜像反射更粗糙。这种模糊应该以非线性方式进行，即纹理的不同部分应该模糊不同。需要这种调整，因为环境贴图纹理表示具有到理想的方向球面空间的非线性映射。两个相邻纹素的中心之间的角距离不是恒定的，立体角也不是由单个纹理像素覆盖。预处理立方体贴图的专用工具，例如AMD的CubeMapGen（现在是开源），在过滤时会考虑这些因素。来自其他面的相邻样本用于创建mipmap链，并且每个纹素的角度范围都被考虑在内。图10.33显示了一个示例。

模糊环境贴图，同时凭经验接近粗糙表面的外观，与实际的BRDF无关。更有原则的方法是在考虑给定的表面法线和视图方向时考虑BRDF函数在球体上采用的形状。然后，我们使用此分布过滤环境贴图。见图10.34。过滤带有镜面波瓣的环境贴图并非易事，因为BRDF可以采用任何形状，具体取决于其粗糙度参数以及视图和法线向量。输入值的至少五个维度（粗糙度和视图和法线方向各自的两个极角）控制得到的波瓣形状。为每个选择存储几个环境贴图是不可行的。

10.5.1 Prefiltered Environment Mapping

应用于光泽材料的环境照明预过滤的实际实施需要使用BRDF的近似值，以便得到的纹理是独立于视图和法向量的。如果我们将BRDF的形状变化仅限制为材质的光泽度，我们可以计算并存储与粗糙度参数的不同选择相对应的一些环境贴图，并选择在运行时使用的适当的环境贴图。在实践中，这意味着限制我们使用的模糊核，并因此限制波瓣形状，以围绕反射矢量径向对称。

想象一下，一些光线从给定的反射视图方向附近进入。直接来自反射视图方向的光将产生最大贡献，随着入射光的方向与反射视图方向的不同而下降。环境贴图纹理区域的面积乘以纹素的BRDF贡献得出该纹理像素的相对效果。该加权贡献乘以环境地图纹理元素的颜色，并将结果相加以计算 $\boldsymbol{q}$。还计算加权贡献的总和s。最终结果 $\boldsymbol{q}/s$是在反射视图方向的波瓣上积分的整体颜色，并存储在生成的反射图中。

如果我们使用Phong模型，径向对称假设自然成立，我们几乎可以精确地计算环境光。Phong凭经验得出了他的模型，与我们在第9.8节中看到的BRDF相比，没有物理动机。Phong的模型和我们在第9.8.1节中讨论的Blinn-Phong BRDF都是余弦波提升到幂，但在Phong着色的情况下，余弦是由反射和视图矢量的点积形成的（公式9.15），而不是半矢量（见公式9.33）和法线。这使得反射波瓣旋转对称。

对于径向对称的镜面波瓣，我们仍然无法容纳的唯一效果是，因为它使得波瓣形状取决于视图方向，是地平线削波。想想看一个闪亮的（不是镜子）球体。例如，在球体表面中心附近看一个对称的Phong叶。查看附近的表面球体的轮廓实际上必须切掉一片叶片，因为地平线下方没有光线可以到达眼睛。见图10.35。这与我们之前在讨论区域照明近似时看到的问题相同（第10.1节），实际上它经常被实时方法忽略。这样做会在掠射角度时产生过亮的阴影。

Heidrich和Seidel 以这种方式使用单个反射贴图来模拟表面的模糊度。为了适应不同的粗糙度级别，通常使用环境立方体贴图的mipmap（第6.2.2节）。每个级别用于存储传入辐射的模糊版本，较高的mip级别存储较粗糙的表面，即较宽的Phong波瓣。在运行期间，我们可以通过使用反射向量来解决立方体贴图，并根据所需的Phong指数（材料粗糙度）强制选择给定的mip级别。见图10.36。

较粗糙的材料使用较宽的过滤区域可以消除高频，因此需要较低的分辨率才能获得足够的结果，从而完美映射到mipmap结构。此外，通过采用GPU硬件的三线性滤波，可以在预滤波的mip级别之间进行采样，模拟我们没有精确表示的粗糙度值。当与菲涅耳术语结合使用时，这种反射贴图对于光泽表面来说效果很好。

出于性能和混叠的原因，要使用的mipmap级别的选择不仅应考虑阴影点处的材质粗糙度，还应考虑由阴影的屏幕像素覆盖区域覆盖的表面区域上的法线和粗糙度的变化。Ashikhmin和Ghosh指出，为了获得最佳结果，应比较两个候选mipmap级别的指数（由纹理硬件计算的缩小级别和对应于当前滤波器宽度的级别），以及应使用较低分辨率的mipmap级别。为了更准确，应该考虑表面方差的扩大效应，并且应该采用对应于最佳拟合像素覆盖区中的平均波瓣的BRDF波瓣的新粗糙度水平。此问题与BRDF抗锯齿（第9.13.1节）完全相同，并且适用相同的解决方案。

前面提出的滤波方案假定给定反射视图方向的所有波瓣具有相同的形状和高度。该假设还意味着叶片必须径向对称。除了地平线上的问题之外，大多数BRDF在所有角度都没有均匀的，径向对称的波瓣。例如，在掠射角处，叶片通常变得更尖锐和更薄。而且，叶片的长度通常随仰角而变化。

对于弯曲表面通常不会感觉到这种效果。然而，对于诸如地板的平坦表面，径向对称的滤波器会引入明显的误差。

Convolving the Environment Map（卷积环境映射）

生成预滤波环境贴图意味着计算每个纹素，对应于方向v，环境辐射与反射lobe D的积分：

$$
\int_\Omega D(\boldsymbol{l,v})L_i(\boldsymbol{l})d\boldsymbol{l}.
$$

该积分是球形卷积（spherical convolution），并且通常不能以分析方式执行，因为对于环境地图而言，$L_i​$ 仅以表格形式已知。一种流行的数值解决方案是采用蒙特卡罗方法：

$$
\int_\Omega D(\boldsymbol{l,v})L_i(\boldsymbol{l})d\boldsymbol{l}\approx\lim_{N\to\infin}\frac1N\sum^N_{k=1}\frac{D(\boldsymbol{l_k,v})L_i(\boldsymbol{l}_k)}{p(\boldsymbol{l}_k,\boldsymbol{v})},\tag{10.36}
$$

其中 $\boldsymbol{l_k}, k = 1,2,...,N$ 代表的是单位球面（方向）上的离散样本，并且 $p(l_k,v)$ 是与在方向 $l_k$ 上生成样本相关联的概率函数。如果我们均匀地对球体进行采样，则 $p(l_k,v)= 1$。虽然这个求和对于我们想要整合的每个方向v是正确的，但是当将结果存储在环境贴图中时，我们还必须考虑投影所带来的失真，通过对每个计算的纹理像素加权它所对应的立体角（参见Driscoll ）。

虽然蒙特卡罗方法简单而正确，但它们可能会将大量样本收敛到积分的数值，即使对于离线过程也可能很慢。这种情况对于mipmap的第一级尤其如此，其中我们编码浅的镜面反射（在Blinn-Phong的情况下为高指数，对于Cook-Torrance为低粗糙度）。我们不仅需要更多的纹素来计算（因为我们需要分辨率来存储高频细节），而且对于不接近完美反射的方向，波瓣可能几乎为零。大多数样品都被“浪费”，因为$D(l_k,v)≈0$。

为了避免这种现象，我们可以使用重要性采样，我们生成方向，其概率分布试图匹配镜面波瓣的形状。这样做是蒙特卡洛积分的常见方差减少技术，并且对于大多数常用的波瓣存在重要性采样策略。对于更有效的采样方案，还可以考虑环境图中辐射的分布以及镜面波瓣的形状。然而，所有依赖点采样的技术通常仅用于离线渲染和地面实例模拟，因为通常需要数百个样本。

为了进一步减少采样方差（noise），我们还可以估计采样之间的距离，并使用锥的总和而不是单个方向进行积分。使用锥体对环境贴图进行采样可以通过对其一个mip级别进行点采样来近似，选择其纹理像素大小跨越类似于锥体的立体角的水平。这样做会引入偏差，但它允许我们大大减少实现无噪声结果所需的样本数量。可以借助于GPU以交互速率执行这种类型的采样。

同样利用面积样本，McGuire等开发了一种技术，旨在实时地近似用镜面反射的卷积结果，而不需要预先计算。该过程通过明智地混合非预先过滤的环境立方体图的多个mipmap级别来完成，以便重建Phong lobe的形状。以类似的方式，Hensley等人使用求和区域表（第6.2.2节）快速执行近似。 McGuire等人和Hensley等人的技术没有任何预先计算，因为在渲染环境地图后，他们仍然需要我们分别生成mip级别或前缀和。对于这两种情况，存在有效算法，因此所需的预计算比执行完全镜面波瓣卷积快得多。这两种技术都足够快，甚至可以实时用于环境照明的表面着色，但它们不如依赖于特殊预过滤的其他方法那么准确。

Kautz等人呈现另一种变型，用于快速生成滤波抛物面反射映射的分层技术。最近，Manson和Sloan使用有效的二次B样条滤波方案显着改进了现有技术，以生成环境地图的mip级别。这些特殊计算的B样条滤波mips然后通过组合几个样本来使用，其方式与McGuire等人和Kautz等人的技术类似，以产生快速和准确的近似。这样做可以实时生成与通过重要性采样蒙特卡罗技术计算的地面实况无法区分的结果。

快速卷积技术允许实时更新预过滤的立方体贴图，这在我们想要过滤的环境贴图动态呈现时是必需的。使用环境贴图经常使得对象难以在不同的照明情况之间移动，例如，从一个房间到另一个房间。可以在帧与帧之间（或每几帧一次）重新生成立方环境贴图，因此如果采用有效的滤波方案，则在新的镜面反射贴图中交换相对便宜。

重新生成完整环境贴图的替代方法是将动态光源的镜面反射高光添加到静态基础环境贴图中。添加的高光可以是预过滤的“斑点”，它们被添加到预过滤的基础环境贴图中。这样做可以避免在运行时进行任何过滤。这些限制是由于环境贴图的假设，灯光和反射的物体是遥远的。所以不要随观察物体的位置而改变。这些要求意味着不能轻易使用局部光源。

如果几何是静态的，但是一些光源（例如太阳）移动，用于更新探针的廉价技术不需要在立方体贴图中动态渲染场景，即将表面属性（位置，法线，材料）存储在G缓冲区环境地图。第20.1节详细讨论了G缓冲区。然后，我们使用这些属性计算表面在环境贴图中的出射辐射。该技术用于使命召唤：无限战争，巫师3 和孤岛惊魂4等。

10.5.2 Split-Integral Approximation for Microfacet BRDFs （微面BRDF的分步积分近似）

环境照明的有用性如此之大，以至于已经开发了许多技术来减少立方体图预滤波中固有的BRDF近似问题。

到目前为止，我们已经描述了通过假设一个Phong lobe然后乘以完美镜像Fresnel术语后的近似值：

$$
\int_{\boldsymbol{l}\in\Omega}f(\boldsymbol{l,v})L_i(\boldsymbol{l})(\boldsymbol{n\cdot l})d\boldsymbol{l}\approx F(\boldsymbol{n,v})\int_\boldsymbol{l\in\Omega}D_{Phong}(\boldsymbol{r})L_i(\boldsymbol{l})(\boldsymbol{n\cdot l})d\boldsymbol{l},\tag{10.37}
$$

其中 $\int_ΩD_{Phong}(\boldsymbol{r})$ 为每个r预先计算到环境立方体图中。如果我们使用公式9.34考虑镜面微平面BRDF $f_{smf}​$，则为了方便重复此过程：

$$
f_{smf}(\boldsymbol{l,v})=\frac{F(\boldsymbol{h,l})G_2(\boldsymbol{l,v,h})D(\boldsymbol{h})}{4\vert\boldsymbol{n\cdot l}\vert\vert\boldsymbol{n\cdot v}\vert}\tag{10.38}
$$

我们注意到，即使假设 $D(h)≈D_{Phong}(r)$ 有效，我们也从照明积分中去除了BRDF的重要部分。也就是阴影项$G_2(1,v,h)$ 和半矢量菲涅耳项 $F(h,l)$，其在积分外的应用没有理论基础。 Lazarov 表明，使用依赖于n·v的完美镜像菲涅耳，而不是像微面BRDF那样的n·h，会产生比完全不使用菲涅耳项更大的误差。Gotanda，Lazarov和Karis独立地推导出类似的split-integral approximation：

$$
\int_\boldsymbol{l\in\Omega}f_{smf}(\boldsymbol{l,v})L_i(\boldsymbol{l})(\boldsymbol{n\cdot l})d\boldsymbol{l}\approx\int_{\boldsymbol{l\in\Omega}}D(\boldsymbol{r})L_i(\boldsymbol{l})(\boldsymbol{n\cdot l})d\boldsymbol{l}\int_{\boldsymbol{l\in\Omega}}f_{smf}(\boldsymbol{l,v})(\boldsymbol{n\cdot l})d\boldsymbol{l}.\tag{10.39}
$$

请注意，即使这个解决方案通常被称为split integral，“我们也不会将积分分解为两个不相交的项，因为这不是一个很好的近似值。记住fsmf包括镜面波瓣D，我们注意到后者以及相反，n·l项在两侧都被复制。在分裂积分近似中，我们在两个积分中包括环境映射中围绕反射向量对称的所有项。Karis称其为split-sum因为它是在他在预计算中使用的重要性采样数值积分器（公式10.36），但实际上它是相同的解决方案。

得到的两个积分都可以有效地预先计算。第一个仅取决于表面粗糙度和反射矢量，假设是径向对称的D波瓣。在实践中，我们可以使用任何波瓣，施加 $\boldsymbol{n = v = r}​$。像往常一样，这个积分可以预先计算并存储在立方体贴图的mip级别中。为了在将半矢量BRDF转换为反射矢量周围的波瓣时在环境光和分析光之间获得类似的亮点，radial-symmetric lobe应使用修改的粗糙度。例如，要使用半角从纯Phong反射向量镜面项转换为Blinn-Phong BRDF，通过将指数除以4得到良好的拟合。

第二个积分是镜面项 $R_{spec}(v)$的半球方向反射（第9.3节）。$R_{spec}$ 函数取决于仰角 $θ$，粗糙度 $α$ 和菲涅耳项 $F$ 。通常使用Schlick近似（公式9.16）来实现F，其仅在单个值 $F_0$ 上参数化，从而使 $R_{spec}$ 成为三个参数的函数。Gotanda以数字方式预先计算$R_{spec}$，将结果存储在三维查找表中。卡里斯和拉扎罗夫指出，$F_0$ 的值可以从$R_{spec}$ 中计算出来，导致两个因子，每个因素取决于两个参数：仰角和粗糙度。Karis将$R_{spec}$的预计算查找减少到可以存储在双通道纹理中的二维表，而Lazarov通过函数拟合推导出对两个因子中的每一个的分析近似。更准确，更简单的分析近似后来由Iwanicki和Pesce推导出来。请注意，$R_{spec}$也可用于提高漫反射BRDF模型的精度（参见第352页的公式9.65）。如果两种技术都在同一个应用程序中实现，那么 $R_{spec}$ 的实现可以用于两者，从而提高效率。

分裂积分解决方案对于恒定的环境贴图是精确的。立方体贴图部件提供缩放镜面反射率的光照强度，这是在均匀照明下正确的BRDF积分。根据经验，卡里斯和拉扎罗夫都观察到近似也适用于一般环境地图，特别是如果频率内容相对较低，这在室外场景中并不罕见。见图10.37。与基本事实相比，这种技术中最大的误差来源是对预滤波环境立方体图的径向对称，非限幅镜面波瓣的限制（图10.35）。 Lagarde建议基于表面粗糙度使用于从反射方向向法线取预滤波环境图的矢量偏斜，因为根据经验，与地面实况相比，这减少了误差。这样做是合理的，因为它部分地补偿了没有用表面进入的辐射半球削波波瓣。

10.5.3 Asymmetric and Anisotropic Lobes（不对称和各向异性的Lobes）

到目前为止我们看到的解决方案都局限于各向同性的镜面波瓣，这意味着当入射和出射方向绕表面法线旋转时（见第9.3节）它们不会发生变化，并且围绕反射向量径向对称。微面BRDF Lobe围绕半矢量 $\boldsymbol{h}$（公式9.33）定义，因此即使在各向同性情况下也不会具有我们需要的对称性。半矢量取决于光方向l，其对于环境照明没有唯一定义。因此，在Karis 之后，对于这些BRDF，我们施加$\boldsymbol{n = v = r}$并得出恒定的粗糙度校正因子，以使镜面高光的大小与原始的半矢量公式相匹配。这些假设都是相当大的误差来源（见图10.38）。

我们在第10.5.1节中提到的一些方法可用于以交互速率计算具有任意BRDF的环境照明，例如来自Luksch等人和Colbert和Kriv'anek的一些方法。然而，由于这些方法需要数十个样本，因此它们很少用于表面的实时着色。相反，它们可被视为蒙特卡洛积分的快速重要性采样技术。

通过在镜面波瓣上施加径向对称来创建预滤波环境贴图，并且通过访问对应于当前表面镜面粗糙度的预滤波瓣的简单直接逻辑，我们的结果仅在直接观察表面时保证是正确的（n = v）。在所有其他情况下，没有这样的保证，并且在掠射角度下，无论BRDF波瓣的形状如何，我们都会产生误差，因为我们忽略了真实的波瓣不能在着色表面点的地平线下方倾斜。通常，镜面反射的确切方向上的数据很可能不是现实的最佳匹配。

Kautz和McCool通过使用存储在预滤波环境图中的径向对称叶片的更好的采样方案来改进之前的预积分。他们提出了两种方法。第一个使用单个样本，但试图找到最好的波瓣在当前视图方向上近似BRDF，而不是依赖于恒定的校正因子。第二种方法平均来自不同叶片的几个样品。第一种方法更好地模拟掠射角度的表面。它们还导出校正因子以解释使用径向对称波瓣近似与原始BRDF相比反射的总能量的差异。第二种解决方案将结果扩展到包括半矢量模型典型的拉伸高光。在这两种情况下，优化技术用于计算驱动预滤波叶片采样的参数表。Kautz和McCool的技术使用贪婪拟合算法和抛物线环境贴图。

最近，Iwanicki和Pesce [807]使用一种称为Nelder-Mead最小化的方法，对GGX BRDF和环境立方体图进行了类似的近似。他们还分析了利用现代GPU的硬件各向异性过滤能力来加速采样的想法。

使用来自预过滤立方体图的单个样本，但使其位置适应更复杂的镜面BRDF峰值的想法，Revie [1489]也探讨了毛发渲染与延迟着色相结合（第20.1节）。在这种情况下，限制并不直接源于环境映射，而是源于在G缓冲区中编码尽可能少的参数的需要。 McAuley [1154]扩展了这个想法，使用这种技术对延迟渲染系统中的所有表面。

McAllister等开发了一种技术，通过利用Lafortune BRDF的特性，能够产生各种效果，包括各向异性和逆向反射。该BRDF 本身是基于物理的渲染的近似。它由多个Phong叶片组成，围绕反射方向扰动。 Lafortune证明了这种BRDF能够通过将这些叶片拟合到He-Torrance模型以及从gonioreflectometer测量真实材料来表示复杂材料。McAllister的技术依赖于注意到，由于Lafortune叶片是广义Phong叶片，因此可以使用传统的预滤波环境图，其mips编码不同的Phong指数。格林等人提出了一种类似的方法，其使用高斯波瓣而不是Phong波瓣。此外，他们的方法可以扩展到支持环境地图的方向阴影（第11.4节）。

10.6 Irradiance Environment Mapping（辐照度环境映射）

上一节讨论了使用过滤环境贴图进行光泽镜面反射。这些图也可用于漫反射。镜面反射的环境贴图具有一些共同的属性，无论它们是未过滤的还是用于镜面反射，或者它们被过滤并用于光泽反射。在这两种情况下，镜面反射环境贴图都使用反射的视图矢量进行索引，并且它们包含辐射值。未过滤的环境贴图包含传入的辐射亮度值，过滤的环境贴图包含传出的辐射亮度值。

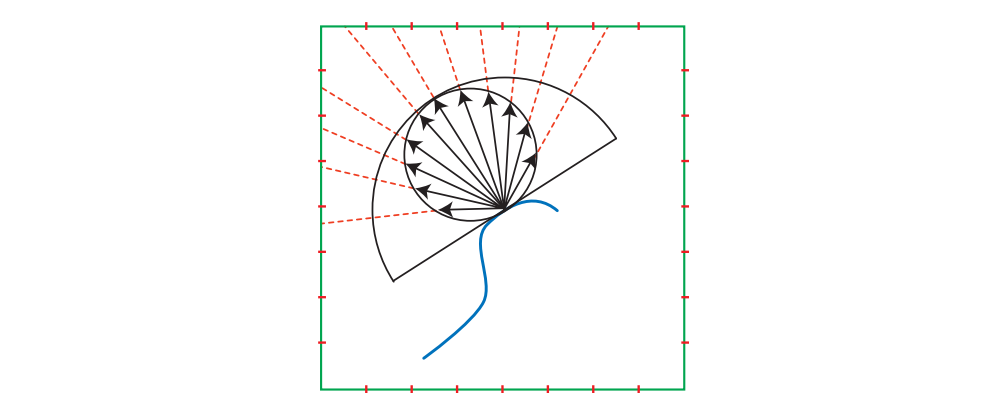
相比之下，漫反射的环境贴图仅使用曲面法线n进行索引，并且它们包含辐照度值。出于这个原因，他们被称为辐照度环境贴图。图10.35显示环境贴图的光泽反射在某些条件下由于其固有的模糊性而存在误差。相同的反射视图矢量可以对应于不同的反射情况。辐照度环境贴图不会发生此问题。曲面法线包含漫反射的所有相关信息。由于与原始照明相比，辐照度环境图极其模糊，因此它们可以以显着较低的分辨率存储。通常使用预滤波镜面环境图的最低mip级别之一来存储辐照度数据。此外，与我们之前研究过的光泽反射不同，我们没有整合到需要被修剪到表面法线周围的半球的BRDF波瓣。环境照明与钳位余弦波瓣的卷积是精确的，而不是近似值。

对于地图中的每个纹素，我们需要总结影响面向给定法线方向的表面的所有照明的余弦加权贡献。通过将覆盖整个可见半球的深远过滤器应用于原始环境映射来创建辐照度环境映射。滤波器包括余弦因子。见图10.39。图10.26中的球体图具有相应的辐照度图，如图10.40所示。使用的辐照度图的一个例子如图10.41所示。

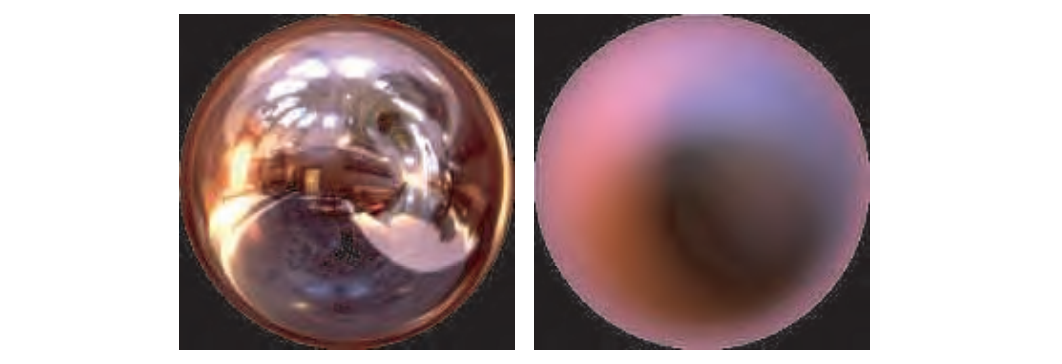
辐照度环境贴图与镜面反射环境或反射贴图分开存储和访问，通常在与视图无关的表示中，例如立方体贴图。见图10.42。而不是反射的视图矢量，表面法线用于访问立方体贴图以检索辐照度。从辐照度环境图中检索的值乘以漫反射率，从镜面反射环境图中检索的值乘以镜面反射率。菲涅耳效应也可以建模，在掠射角增加镜面反射（并可能降低漫反射）。

由于辐照度环境图使用极宽的滤波器，因此难以通过采样在运行中有效地创建它们。 King 讨论了如何在GPU上执行卷积以创建辐照度图。通过将环境地图转换为频域，他能够在2004年代硬件上以超过300 FPS的速率生成辐照度图。

用于漫射或粗糙表面的滤波环境地图可以以低分辨率存储，但是有时也可以从场景的相对小的反射贴图生成，例如64×64纹素的立方体贴图面。这种方法的一个问题是渲染成这种小纹理的区域光源可能会落在纹理像素之间，“导致光线完全闪烁或褪色。为了避免这个问题，Wiley和Scheuermann建议代表这种光渲染动态环境贴图时，通过巨大的“卡片”（纹理矩形）来源。

与光泽反射的情况一样，动态光源也可以添加到预滤光辐照度环境图中。 Brennan给出了一种廉价的方法。想象一下单个光源的辐照度图。在光的方向上，当光线直接照射到表面上时，辐射是最大的。给定表面法线方向（即给定纹理像素）的辐射度随着与光的角度的余弦而下降，并且在表面背离光的情况下为零。 GPU可用于通过渲染半球（表示以观察者为中心的余弦波）以及沿着光线方向的半球极点，将该贡献直接快速添加到现有的辐照度图。

10.6.1 Spherical Harmonics Irradiance （球谐函数辐照度）

虽然我们已经讨论了仅使用诸如立方体贴图之类的纹理来表示辐照度环境贴图，但是其他表示也是可能的，如第10.3节中所示。特别是球面谐波作为辐照度环境贴图表示非常流行，因为来自环境照明的辐照度是平滑的。利用余弦波瓣进行辐射会导致从环境映射中去除所有高频分量。

Ramamoorthi和Hanrahan表明，只用前九个SH系数（每个系数是RGB矢量，因此我们需要存储27个浮点数），辐照度环境图可以表示为误差在1％的精度。然后可以将任何辐照度环境图解释为球函数 $E(\boldsymbol{n})$ 并使用等式10.21和10.23投影到九个RGB系数上。这种形式比立方体或抛物线图更紧凑，在渲染过程中，可以通过计算一些简单的多项式来重建辐照度，而不是访问纹理。通常，如果辐照度环境图表示间接照明（交互式应用中的常见情况），则需要较低的精度。在这种情况下，对于恒定基函数和三个线性基函数，四个系数通常可以产生良好的结果，因为间接照明倾向于低频，即随角度缓慢变化。

Ramamoorthi和Hanrahan 还表明，通过将每个系数乘以常数，可以将入射辐射函数 $L(\boldsymbol{l})​$ 的SH系数转换成辐照度函数 $E(\boldsymbol{n})​$ 的系数。这样做可以快速地将环境贴图过滤到辐照度环境贴图中，即将它们投影到SH基础中，然后将每个系数乘以常数。例如，这是King的快速辐照度滤波实现的工作原理。该想法是从辐射度计算辐照度等效于在进入辐射函数 $L(\boldsymbol{l})​$ 和钳位余弦函数 $cos(θ_i)^+​$之间执行球形卷积。由于钳位余弦函数关于球体的z轴旋转对称，因此它在SH中呈现特殊形式：其投影在每个频带中仅具有一个非零系数。非零系数对应于图10.21（第401页）中间列中的基函数，也称为区域谐波（zonal harmonics）。

在一般球函数和旋转对称函数（例如钳位余弦函数）之间执行球面卷积的结果是球体上的另一个函数。可以在函数的SH系数上有效地执行该卷积。卷积结果的SH系数等于两个函数的系数的乘积（乘法），由 $\sqrt{4π/(2l + 1)}$缩放，其中 $\boldsymbol{l}$ 是频带索引。然后，辐照度函数$E(\boldsymbol{n})$的SH系数等于辐射函数 $L(\boldsymbol{l})$ 的系数乘以钳位余弦函数 $cos(θ_i)^+$ 的系数，由频带常数缩放。超过前九个的 $cos(θ_i)^+$ 系数具有小值，这解释了为什么九个系数足以表示辐照度函数 $E(\boldsymbol{n})$ 。可以以这种方式快速评估SH辐照度环境图。 Sloan描述了一种有效的GPU实现。

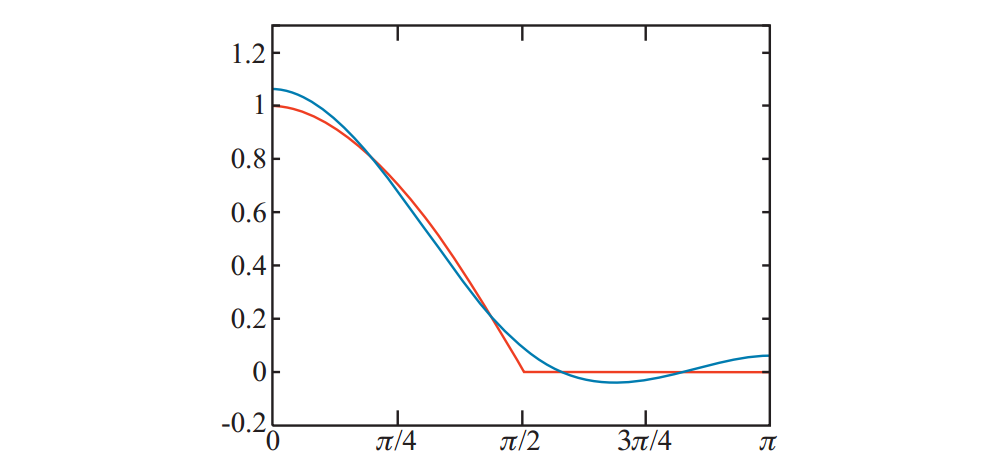
这里有一个固有的近似，因为虽然 $E(\boldsymbol{n})​$ 的高阶系数很小，但它们不是零。见图10.43。近似值非常接近，尽管π= 2和π之间的曲线的“摆动”应该为零，在信号处理中称为振铃。通常在高频函数近似少量的情况下发生。基本函数，如第10.3.2节所示。在π= 2时钳位为零是一个急剧变化，这意味着我们的钳位余弦函数具有无限频率信号。在大多数情况下振铃不明显，但可以看出极端的光照条件，如物体阴影侧的颜色变化或明亮\斑点。如果辐照度环境贴图用于仅存储间接照明（经常发生），则振铃不太可能成为问题。有一些预过滤方法可以最大限度地减少问题。见图10.44。

图10.40显示了直接导出的辐照度图如何与由九项函数合成的辐照度图进行比较。该SH表示可以在渲染期间使用当前曲面法线 n 进行评估，或者可以用于快速创建立方体或抛物线图以供以后使用。这种照明便宜并且为漫射情况提供了良好的视觉效果。

动态渲染的三次环境地图可以投影到SH基础上。由于三次环境贴图是入射辐射函数的离散表示，因此公式10.21中球面上的积分成为立方体贴图纹素的总和：

$$
k_{Lj}=\sum_tf_j(\boldsymbol{r}[t])L[t]d\omega[t],\tag{10.40}
$$

其中t是当前立方体贴图纹理元素的索引，$\boldsymbol{r}[t]$ 是指向当前纹素的方向向量，$f_j(\boldsymbol{r}[t]) $是在 $\boldsymbol{r}[t]$ 处计算的第j个SH基函数，$L[t]$ 是纹素中存储的辐射，$d\omega[t]$ 是纹素对应的立体角。Kautz，King和Sloan描述了如何计算 $d\omega[t]$。

$$
k_{Ej}=k'_{\cos+j}k_{Lj}=k'_{\cos+j}\sum_tf_j(\boldsymbol{r}[t])L[t]d\omega[t],\tag{10.41}
$$

其中 $k_{Ej}​$ 是辐照度函数 $E(\boldsymbol{n})​$ 的第 $j​$ 个系数，$k_{Lj}​$ 是入射辐射函数 $L(\boldsymbol{l})​$ 的第j个系数，$k_{\cos+j}​$ 是钳位余弦函数 $cos(θ_i)^+​$ 的第 $j​$ 个系数通过 $\sqrt{4π/(2l + 1)}​$（$l​$ 是频带指数）。

给定t和立方体图分辨率，因子 $k'_{\cos+j}f_j(\boldsymbol{r}[t])d\omega[t]$ 对于每个基函数 $f_j()$ 是恒定的。这些基本因子可以离线预先计算并存储在立方体贴图中，立方体贴图的分辨率应与将要渲染的动态环境贴图的分辨率相同。通过在每个颜色通道中打包单独的基础因子，可以减少使用的纹理数量。为了计算动态立方体贴图的辐照度系数，将适当的基本因子图的纹素与动态立方体贴图的纹素相乘，并将结果相加。除了关于动态辐照度立方体贴图的信息之外，King还提供了关于GPU SH投影的实现细节。

可以将动态光源添加到现有的SH辐照度环境地图中。这种合并是通过计算灯的辐照度贡献的SH系数并将它们加到现有系数来完成的。这样做可以避免重新计算整个辐照度环境贴图的需要。这是一个简单的过程，因为存在点，圆盘和球面光系数的简单解析表达式。对系数求和与对辐照度求和具有相同的效果。通常，这些表示以带状谐波给出，对于与z轴对准的光，然后可以应用旋转以将光定向到任意方向。带状谐波旋转是SH旋转的一个特例（第10.3.2节），效率更高，只需要一个点积而不是全矩阵变换。具有更复杂形状的光源的系数可以通过将它们绘制成图像然后以数字方式投影到SH基础上来计算。对于物理天空模型的特殊情况，Habel展示了Preetham天窗在球谐函数中的直接扩展。

将普通分析光源投射到SH中的容易性是重要的，因为通常环境照明用于代替远距离或不太强烈的光源。补光灯是一个重要的案例。在渲染中，放置这些光源以模拟场景中的间接光，即从表面反射的光。通常不计算填充光的镜面贡献，特别是因为这些光相对于阴影对象可以在物理上较大并且与场景中的其他照明源相比相对暗淡。这些因素使他们的镜面高光更加分散，不那么引人注目。这种类型的灯在电影和视频的照明中具有真实世界的类比，其中物理补光（fill lights）通常用于在阴影中添加照明。

在球谐波空间中，进行相反的推导也很简单，即从SH中投射的辐射中提取分析光源。在他对SH技术的调查中，Sloan 展示了如果给定具有已知轴的定向光源，很容易从SH辐照度表示计算光应该具有的强度以最小化其自身与编码辐照度之间的误差。

在他之前的工作中斯隆展示了如何通过仅使用第一（线性）波段中的系数来选择近似最佳方向。调查还包括一种提取多个方向灯的方法。这项工作表明球谐函数是光总和的实用基础。我们可以将多个灯投射到SH中并提取较少数量的方向灯，这些灯可以近似于投影组。 lightcuts框架提供了聚合不太重要的灯光的原则方法。

虽然最常用于辐照度，但SH投影可用于模拟光滑的，视图相关的BRDF照明。 Ramamoorthi和Hanrahan描述了一种这样的技术。它们不是单一颜色，而是在立方体图中存储编码环境地图的视图依赖性的球面谐波投影的系数。但是，在实践中，这种技术比我们之前看到的预过滤环境贴图方法需要更多的空间。Kautz等人使用SH系数的二维表导出更经济的解决方案，但是该方法限于相当低频的照明。

10.6.2 Other Representation（其他）

尽管立方体贴图和球面谐波是辐照度环境贴图的最常用表示，但其他表示也是可能的。见图10.45。许多辐照度环境地图有两种主要颜色：顶部的天空颜色和底部的底色。受此观察的启发，Parker等人呈现仅使用两种颜色的半球照明模型。假设上半球发出均匀的辐射亮度 $L_{sky}$，并假设下半球发出均匀的辐射 $L_{ground}$。这种情况下的辐照度积分是

$$
E=
\begin{cases}
\pi((1-\frac12\sin\theta)L_{sky}+\frac12\sin\theta L_{ground}),;where;\theta\lt90^\circ,\\
\pi(\frac12\sin\theta L_{sky}+(1-\frac12\sin\theta) L_{ground}),;where;\theta\ge90^\circ,
\end{cases}\tag{10.42}
$$

其中θ是表面法线和天空半球轴之间的角度。 Baker和Boyd提出了更快的近似（由Taylor描述）：

$$
E=\pi(\frac{1+\cos\theta}2L_{sky}+\frac{1-\cos\theta}2L_{ground}),\tag{10.43}
$$

这是天空和地面之间的线性插值，使用 $(cosθ+ 1)/2$ 作为插值因子。术语cosθ通常快速计算为点积，并且在天空半球轴是基本轴之一（例如，y轴或z轴）的常见情况下，不需要计算全部，因为它等于n的世界空间坐标之一。近似值相当接近并且明显更快，因此对于大多数应用来说，它更适合于完整表达式。

Forsyth提出了一种廉价而灵活的照明模型，称为trilight，它包括定向，双向，半球形和环绕照明作为特殊情况。

Valve最初引入了辐照度的环境立方体表示（第10.3.1节）。通常，我们在第10.3节中看到的所有球面函数表示都可用于预先计算的辐照度。对于辐照度函数所代表的低频信号，我们知道SH是一个很好的近似。我们倾向于创建特殊方法来简化或使用比球谐波更少的存储。

如果我们想要计算遮挡和其他全局照明效果，或者如果我们想要合并光泽反射（第10.1.1节），则需要更复杂的高频表示。预计算照明以考虑所有相互作用的一般概念称为预计算辐射传输（PRT），将在第11.5.3节中讨论。捕获高频率的光泽照明也称为全频照明。小波表示通常在此上下文中使用作为压缩环境贴图的方法，并且以类似于球谐函数的方式设计有效的算子。Ng等人展示了使用 Haar小波（haar wavelets） 来推广辐照度环境映射以模拟自阴影。它们以小波为基础存储环境贴图和阴影函数，它们在对象表面上变化。这种表示是值得注意的，因为它相当于环境立方体图的变换，执行每个立方体面的二维小波投影。因此，它可以被视为立方体贴图的压缩技术。

10.7 Sources of Error （误差来源）

为了正确执行着色，我们必须计算非点源光上的积分。在实践中，这一要求意味着我们可以根据所考虑的灯的特性采用许多不同的技术。通常，实时引擎可以分析地模拟一些重要的光，在光区域上近似积分并通过阴影图计算遮挡。所有其他光源，如远距离照明，天空，补光和光在表面上反射，通常由镜面反射分量的环境立方体贴图和漫反射辐照度的球面基础表示。

采用混合技术进行照明意味着我们永远不会直接使用给定的BRDF模型，但具有不同程度的误差的近似值。有时BRDF近似是明确的，因为我们拟合中间模型以计算光照积分——LTC就是一个例子。其他时候，我们在某些（通常是罕见的）条件下构建对于给定BRDF精确的近似值，但一般会出现误差，预滤波的立方体贴图属于此类别。

在开发实时着色模型时要考虑的一个重要方面是确保不同形式的照明之间的差异不明显。具有来自不同表示的相干光可能在视觉上比每个所呈现的绝对近似误差更重要。

遮挡对于逼真的渲染也是至关重要的，因为光线“泄漏”应该没有的地方往往比不应该有光的地方更明显。大多数区域的光线表示对于阴影来说并不是微不足道的。今天没有任何实时遮蔽技术，即使在考虑“软化”效果（第7.6节）时，也能准确地考虑光的形状。我们计算一个标量因子，当一个物体投射阴影时，我们将它们相乘以减少给定光线的贡献，这是不正确的；我们应该在与BRDF进行整合时考虑这种遮挡。环境照明的情况特别困难，因为我们没有明确的主导光方向，因此不能使用点源光的遮蔽技术。

即使我们已经看到一些相当先进的照明模型，重要的是要记住这些并不是真实世界照明源的精确表示。例如，在环境照明的情况下，我们假设辐射源无限远，这是永远不可能的。我们所看到的所有分析灯都在一个更强大的假设上工作，即灯在其表面上的每个点上均匀地在出射半球上发出辐射。在实践中，这种假设可能是错误的来源，因为真正的灯光通常具有很强的方向性。在摄影和电影照明中，经常使用特制的面具和过滤器（称为图案片，黄瓜或饼干）来产生艺术效果。例如，摄影师格雷戈里·克鲁兹森（Gregory Crewdson）参见图10.46中的复杂电影摄影。为了在保持大面积发射的同时限制照明角度，可以在大型发光面板（所谓的柔光箱）的前面添加称为蜂窝的屏蔽黑色材料的网格。镜子和反射器的复杂配置也可用于灯具的外壳，例如室内照明，汽车前灯和手电筒。见图10.47。这些光学系统产生远离物理中心辐射光的一个或多个虚拟发射器，并且在执行衰减计算时应考虑该偏移。

请注意，应始终在感知的，面向结果的框架中评估这些错误（除非我们的目标是进行预测渲染，即可靠地模拟曲面的真实世界外观）。在艺术家的手中，某些简化，即使不现实，仍然可以产生有用和富有表现力的原语。物理模型在使艺术家更容易创建视觉上合理的图像时非常有用，但它们并不是他们自己的目标。

Further Reading and Resources

“Light Science and Magic: An Introduction to Photographic Lighting ”一书是理解真实世界摄影灯的绝佳参考。对于电影照明Set Lighting Technician’s Handbook: Film Lighting Equipment, Practice, and Electrical Distribution 是一个很好的介绍。

Debevec在图像照明领域开创的工作对于需要从真实世界场景捕捉环境地图的人来说非常感兴趣。
SIGGRAPH 2003课程以及Reinhard等人的High Dynamic Range Imaging: Acquisition, Display, and Image-Based Lighting 一书涵盖了大部分这项工作。

可以帮助模拟的一种资源是光配置文件。照明工程学会（IES）发布了照明测量的手册和文件格式标准。这种格式的数据通常可从许多制造商处获得。 IES标准仅限于通过其角度发射轮廓描述光。它没有完全模拟光学系统对衰减的影响，也没有模拟光表面区域的发射。

Szirmay-Kalos 关于镜面反射效应的最新报告包括许多对环境绘图技术的参考。

（Chapter 10 End.）